题目内容
1.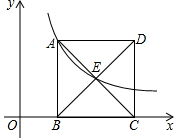 如图,正方形ABCD的边长为4,边BC在x轴上,点E是对角线AC,BD的交点,反比例函数y=$\frac{k}{x}(x>0)$的图象经过A,E两点,则k的值为( )
如图,正方形ABCD的边长为4,边BC在x轴上,点E是对角线AC,BD的交点,反比例函数y=$\frac{k}{x}(x>0)$的图象经过A,E两点,则k的值为( )| A. | 8 | B. | 4 | C. | 6 | D. | 3 |
分析 设B(a,0),则C(a+4,0),A(a,4),利用正方形的性质得点E为AC的中点,则可表示出E(a+2,2),然后利用反比例函数图象上点的坐标特征得到k=4a=2(a+2),再求出a后易得k的值.
解答 解:设B(a,0),则C(a+4,0),A(a,4),
∵点E为正方形ABCD的对角线的交点,
∴点E为AC的中点,
∴E(a+2,2),
∵点A和点E在反比例函数y=$\frac{k}{x}(x>0)$的图象上,
∴k=4a=2(a+2),解得a=2,
∴k=8.
故选A.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了正方形的性质.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
11.吉林省春节黄金周期间,共接待游客8 897 700,这个数字用科学记数法表示为( )
| A. | 88.977×105 | B. | 8.8977×106 | C. | 0.88977×103 | D. | 8.897×103 |
12.二次函数y=ax2+bx+c的y与x的部分对应值如表:
则下列判断中正确的是( )
| X | … | 0 | 1 | 3 | 4 | … |
| y | … | 2 | 4 | 2 | -2 | … |
| A. | 抛物线开口向上 | B. | y最大值为4 | ||
| C. | 当x>1时,y随著x的增大而减小 | D. | 当0<x<2时,y>2 |
16. 如图是一个几何体的三视图,则该几何体是( )
如图是一个几何体的三视图,则该几何体是( )
 如图是一个几何体的三视图,则该几何体是( )
如图是一个几何体的三视图,则该几何体是( )| A. | 圆柱 | B. | 圆锥 | C. | 正三棱柱 | D. | 正三棱锥 |
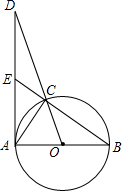 如图,已知AB是⊙O的直径,点C为圆上一点,点D在OC的延长线上,连接DA,交BC的延长线于点E,使得∠DAC=∠B.
如图,已知AB是⊙O的直径,点C为圆上一点,点D在OC的延长线上,连接DA,交BC的延长线于点E,使得∠DAC=∠B.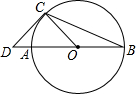 如图,AB是⊙O的直径,BC是弦,连结OC,过点C的切线交BA的延长线于点D,若OC=CD=2,则$\widehat{BC}$的长是$\frac{3π}{2}$.(结果保留π)
如图,AB是⊙O的直径,BC是弦,连结OC,过点C的切线交BA的延长线于点D,若OC=CD=2,则$\widehat{BC}$的长是$\frac{3π}{2}$.(结果保留π)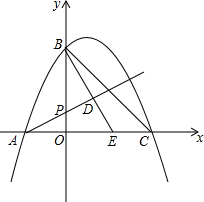 已知在平面直角坐标系xOy(如图)中,抛物线y=-x2+bx+c与x轴交于点A(-1,0)与点C(3,0),与y轴交于点B,点P为OB上一点,过点B作射线AP的垂线,垂足为点D,射线BD交x轴于点E.
已知在平面直角坐标系xOy(如图)中,抛物线y=-x2+bx+c与x轴交于点A(-1,0)与点C(3,0),与y轴交于点B,点P为OB上一点,过点B作射线AP的垂线,垂足为点D,射线BD交x轴于点E. 如图是有关x的代数式的方阵,若第10行第2项的值为1034,则此时x的值为2.
如图是有关x的代数式的方阵,若第10行第2项的值为1034,则此时x的值为2.