题目内容
8. 如图,在矩形ABCD中,E是BC边的中点,沿直线AE翻折△ABE,使B点落在点F处,连结CF并延长交AD于G点.
如图,在矩形ABCD中,E是BC边的中点,沿直线AE翻折△ABE,使B点落在点F处,连结CF并延长交AD于G点.(1)依题意补全图形;
(2)连接BF交AE于点O,判断四边形AECG的形状并证明;
(3)若BC=10,AB=$\frac{20}{3}$,求CF的长.
分析 (1)结合题意即可补全图形;
(2)由折叠的性质可得点O是BF中点,又由E是BC边的中点,可得EO是△BCF的中位线,即可判定EO∥CG.又由AG∥CE,即可得四边形AECG是平行四边形;
(3)首先由勾股定理求得AE的长,然后由三角形的面积相等,求得BO的长,继而求得BF的长,又由勾股定理,求得答案.
解答 (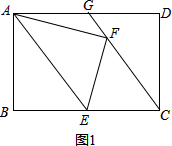 1)解:依题意补全图形,如图1;
1)解:依题意补全图形,如图1;
(2)四边形AECG是平行四边形.
证明:如图2,依翻折的性质可知,点O是BF中点,
∵E是BC中点,
∴EO∥CG.
∵AG∥CE,
∴四边形AECG是平行四边形.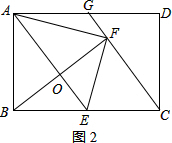 (3)解:在Rt△ABE中,BE=$\frac{1}{2}$BC=$\frac{1}{2}$×10=5,AB=$\frac{20}{3}$,
(3)解:在Rt△ABE中,BE=$\frac{1}{2}$BC=$\frac{1}{2}$×10=5,AB=$\frac{20}{3}$,
∴AE=$\sqrt{A{B}^{2}+B{E}^{2}}$=$\frac{25}{3}$.
∵S△ABE=$\frac{1}{2}$AB•BE=$\frac{1}{2}$AE•BO,
∴BO=4.
∴BF=2BO=8.
∵BF⊥AE,AE∥CG,
∴∠BFC=90°.
∴CF=$\sqrt{B{C}^{2}-B{F}^{2}}$=6.
点评 此题考查了矩形的性质、平行四边形的判定、折叠的性质以及勾股定理等知识.注意结合题意准确画出图形,利用面积法求解是关键.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
19.为了备战2016年里约奥运会,中国射击队正在积极训练.甲、乙两名运动员在相同的条件下,各射击10次.经过计算,甲、乙两人成绩的平均数均是9.5环,甲的成绩方差是0.125,乙的成绩的方差是0.85,那么这10次射击中,甲、乙成绩的稳定情况是( )
| A. | 甲较为稳定 | B. | 乙较为稳定 | ||
| C. | 两个人成绩一样稳定 | D. | 不能确定 |
3.在平面直角坐标系中.点P(1,-2)关于x轴对称的点的坐标是( )
| A. | (1,2) | B. | (-1,-2) | C. | (-1,2) | D. | (-2,1) |
13. 如图,在菱形ABCD中,∠ABC=120°,点E是边AB的中点,P是对角线AC上的一个动点,若AB=2,则PB+PE的最小值是( )
如图,在菱形ABCD中,∠ABC=120°,点E是边AB的中点,P是对角线AC上的一个动点,若AB=2,则PB+PE的最小值是( )
 如图,在菱形ABCD中,∠ABC=120°,点E是边AB的中点,P是对角线AC上的一个动点,若AB=2,则PB+PE的最小值是( )
如图,在菱形ABCD中,∠ABC=120°,点E是边AB的中点,P是对角线AC上的一个动点,若AB=2,则PB+PE的最小值是( )| A. | 1 | B. | $\sqrt{3}$ | C. | 2 | D. | $2\sqrt{3}$ |
 有这样一个问题:如图,在四边形ABCD中,AB=AD,CB=CD,我们把这种两组邻边分别相等的四边形叫做筝形.请探究筝形的性质与判定方法.
有这样一个问题:如图,在四边形ABCD中,AB=AD,CB=CD,我们把这种两组邻边分别相等的四边形叫做筝形.请探究筝形的性质与判定方法.