题目内容
17.已知抛物线y=x2+px+q与x轴的正半轴交于点A(x1,0)和B(x2,0)两点,x1,x2均为整数,且x1≠x2,p+q=8,则x${\;}_{1}^{2}$+x${\;}_{2}^{2}$=104.分析 由图象与x轴交于点A(x1,0)、B(x2,0)两点,就相当于方程x2+px+q=0两个根分别为x1,x2,由两根关系求解即可.
解答 解:∵抛物线y=x2+px+q与x轴的正半轴交于点A(x1,0)和B(x2,0)两点,
∴x1>0,x2>0,
∴x1x2=q>0,x1+x2=-p>0.
∴x12+x22=(x1+x2)2-2x1x2=(-p)2-2q=p2-2(8-p)=p2+2p-16=(p+1)2-17>0,
∴p+1<-$\sqrt{17}$,
∴p+1<-4
∴p<-5,
∵x1,x2均为整数,且x1≠x2,p+q=8,
∴p=-6,q=14,或p=-7,q=15或p=-8,q=16或p=-10,q=18或p=-12,q=20,
只有p=-12,q=20时,符合题意,
∴x12+x22=(p+1)2-17=(-12+1)2-17=104.
故答案为104.
点评 考查了抛物线与x轴的交点.注意使用一元二次方程根与系数的关系求解关于两根的问题.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
6.在半径为6的⊙O中,60°圆心角所对的弧长是( )
| A. | π | B. | 2π | C. | 4π | D. | 6π |
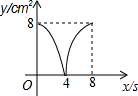
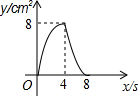
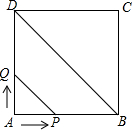 如图,正方形ABCD的边长为4cm,动点p,Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间函数关系可以用图象表示为( )
如图,正方形ABCD的边长为4cm,动点p,Q同时从点A出发,以1cm/s的速度分别沿A→B→C和A→D→C的路径向点C运动,设运动时间为x(单位:s),四边形PBDQ的面积为y(单位:cm2),则y与x(0≤x≤8)之间函数关系可以用图象表示为( )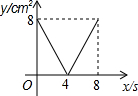
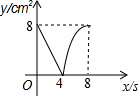
 如图所示,将正五边形ABCDE绕点C按顺时针方向最少旋转72度后顶点D会落在直线BC上.
如图所示,将正五边形ABCDE绕点C按顺时针方向最少旋转72度后顶点D会落在直线BC上.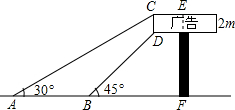 如图,某广告牌竖直矗立在水平地面上,经测量,得到如下相关数据:CD=2m,∠CAB=30°,∠DBF=45°,AB=10m,则广告牌的高EF=(4$\sqrt{3}$+4)m.(结果保留根号)
如图,某广告牌竖直矗立在水平地面上,经测量,得到如下相关数据:CD=2m,∠CAB=30°,∠DBF=45°,AB=10m,则广告牌的高EF=(4$\sqrt{3}$+4)m.(结果保留根号)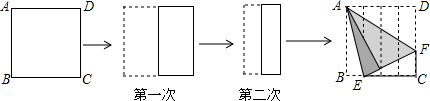
 如图,在△ABC中,∠A=30°,∠B=55°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的B′处
如图,在△ABC中,∠A=30°,∠B=55°,D是AB上一点,将△ABC沿CD折叠,使B点落在AC边上的B′处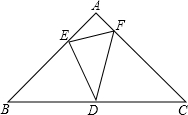 已知△ABC是等腰直角三角形,∠A=90°,AB=$\sqrt{2}$,点D位于边BC的中点上,点E在AB上,点F在AC上,∠EDF=45°.
已知△ABC是等腰直角三角形,∠A=90°,AB=$\sqrt{2}$,点D位于边BC的中点上,点E在AB上,点F在AC上,∠EDF=45°.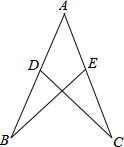 如图,点D在AB上,点E在AC上,AB=AC,AD=AE.求证:BE=CD.
如图,点D在AB上,点E在AC上,AB=AC,AD=AE.求证:BE=CD.