题目内容
5. 如图所示,将正五边形ABCDE绕点C按顺时针方向最少旋转72度后顶点D会落在直线BC上.
如图所示,将正五边形ABCDE绕点C按顺时针方向最少旋转72度后顶点D会落在直线BC上.
分析 利用正五边形的性质得出∠BCD=108°,进而得出旋转的最小角度.
解答 解:∵正五边形ABCDE,
∴∠BCD=108°,
∴将正五边形ABCDE绕点C按顺时针方向最少旋转72度后顶点D会落在直线BC上.
故答案为:72.
点评 此题主要考查了旋转的性质以及正五边形的性质,得出∠BCD的度数是解题关键.

练习册系列答案
相关题目
14.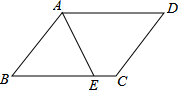 如图,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
如图,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
 如图,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )
如图,?ABCD的周长为20cm,AE平分∠BAD,若CE=2cm,则AB的长度是( )| A. | 10cm | B. | 8cm | C. | 6cm | D. | 4cm |
20.把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6cm,DC=7cm,把三角板DCE绕点C顺时针旋转15°得到△D1CE1,如图乙所示,此时AB与CD1相交于点O,与D1E1相交于点F,则线段AD1的长度是( )
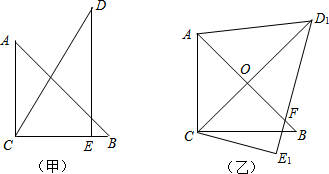

| A. | 3$\sqrt{2}$ | B. | 5 | C. | 4 | D. | $\sqrt{31}$ |
14.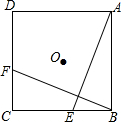 如图,E,F分别是正方形ABCD的边BC,CD上的点,CD上的点,BE=CF,连接AE,BF,将△ABE绕正方形的对角线的交点O按顺时针方向旋转到△BCF,则旋转角是( )
如图,E,F分别是正方形ABCD的边BC,CD上的点,CD上的点,BE=CF,连接AE,BF,将△ABE绕正方形的对角线的交点O按顺时针方向旋转到△BCF,则旋转角是( )
 如图,E,F分别是正方形ABCD的边BC,CD上的点,CD上的点,BE=CF,连接AE,BF,将△ABE绕正方形的对角线的交点O按顺时针方向旋转到△BCF,则旋转角是( )
如图,E,F分别是正方形ABCD的边BC,CD上的点,CD上的点,BE=CF,连接AE,BF,将△ABE绕正方形的对角线的交点O按顺时针方向旋转到△BCF,则旋转角是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
15.一个物体作左右方向的运动,规定向右运动4m记作+4m,那么向左运动4m记作( )
| A. | -4m | B. | 4m | C. | 8m | D. | -8m |

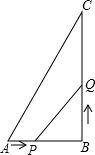 如图所示,在△ABC中∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,点Q从点B开始沿BC边向点C以2cm/s的速度运动.
如图所示,在△ABC中∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,点Q从点B开始沿BC边向点C以2cm/s的速度运动.