题目内容
12.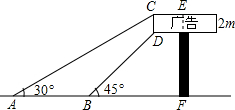 如图,某广告牌竖直矗立在水平地面上,经测量,得到如下相关数据:CD=2m,∠CAB=30°,∠DBF=45°,AB=10m,则广告牌的高EF=(4$\sqrt{3}$+4)m.(结果保留根号)
如图,某广告牌竖直矗立在水平地面上,经测量,得到如下相关数据:CD=2m,∠CAB=30°,∠DBF=45°,AB=10m,则广告牌的高EF=(4$\sqrt{3}$+4)m.(结果保留根号)
分析 过点D作DG⊥AF于点G,设DG=xm,则CG=(x+2)m,解Rt△BGD,得出BG=DG=xm,则AG=BG+AB=(x+10)m.再解Rt△AGC,由tan30°=$\frac{GC}{AG}$,得出$\frac{x+2}{x+10}$=$\frac{\sqrt{3}}{3}$,解方程求出x的值,进而得出EF.
解答 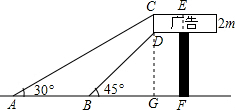 解:如图,过点D作DG⊥AF于点G,
解:如图,过点D作DG⊥AF于点G,
设DG=xm,则CG=(x+2)m,
在Rt△BGD中,∵∠BGD=90°,∠DBG=45°,
∴BG=DG=xm,
∴AG=BG+AB=(x+10)m.
在Rt△AGC中,∵∠AGC=90°,∠CAG=30°,
∴tan30°=$\frac{GC}{AG}$,
∴$\frac{x+2}{x+10}$=$\frac{\sqrt{3}}{3}$,
∴x=4$\sqrt{3}$+2,
∴EF=CG=CD+DG=2+4$\sqrt{3}$+2=4$\sqrt{3}$+4(m)
答:广告牌的高EF=(4$\sqrt{3}$+4)m.
故答案为(4$\sqrt{3}$+4).
点评 此题主要考查了解直角三角形的应用,根据已知构造直角三角形得出DG的长是解题的关键.

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
1.一个正常人的心跳平均每分70次,一天大约跳100800次,将100800用科学记数法表示为( )
| A. | 0.1008×106 | B. | 1.008×106 | C. | 1.008×105 | D. | 10.08×104 |
20.把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6cm,DC=7cm,把三角板DCE绕点C顺时针旋转15°得到△D1CE1,如图乙所示,此时AB与CD1相交于点O,与D1E1相交于点F,则线段AD1的长度是( )
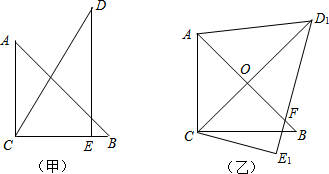

| A. | 3$\sqrt{2}$ | B. | 5 | C. | 4 | D. | $\sqrt{31}$ |
7.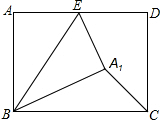 如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD的平分线上时,CA′的长为( )
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD的平分线上时,CA′的长为( )
 如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD的平分线上时,CA′的长为( )
如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A′恰好落在∠BCD的平分线上时,CA′的长为( )| A. | 3或4$\sqrt{2}$ | B. | 3$\sqrt{2}$或4$\sqrt{2}$ | C. | 3或4 | D. | 4或3$\sqrt{2}$ |