题目内容
2.如图,折叠正方形ABCD纸片,第一次对折,第二次又对折;展开后压平,最后把△ABE、△ADF按图折叠,(1)则∠EAF的度数45°;
(2)已知AB=1,则CF=$\frac{2}{5}$.
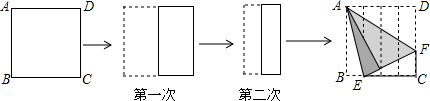
分析 (1)根据折叠的性质,知∠BAE=∠GAE,∠DAF=∠GAF,所以∠EAF=$\frac{1}{2}$∠BAD=45°;
(2)由图形知EC=$\frac{3}{4}$,BE=EG=$\frac{1}{4}$,设CF=x,则DF=FG=1-x,根据勾股定理列方程即可得解.
解答 解:(1)根据折叠的性质可知∠BAE=∠GAE,∠DAF=∠GAF,
∴∠EAF=∠GAE+∠GAF=$\frac{1}{2}$∠BAD=45°;
故答案为:45°.
(2)由题意知,EC=$\frac{3}{4}$,BE=EG=$\frac{1}{4}$,
设CF=x,则DF=FG=1-x,EF=(1-x)+$\frac{1}{4}$=$\frac{5}{4}$-x,
∴x2+($\frac{3}{4}$)2=($\frac{5}{4}$-x)2,
解得:x=$\frac{2}{5}$.
故答案为:$\frac{2}{5}$.
点评 本题是一道有关折叠的试题,考查了轴对称的性质及运用,直角三角形的性质,勾股定理,题目设计比较新颖,难度一般.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.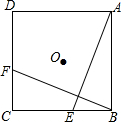 如图,E,F分别是正方形ABCD的边BC,CD上的点,CD上的点,BE=CF,连接AE,BF,将△ABE绕正方形的对角线的交点O按顺时针方向旋转到△BCF,则旋转角是( )
如图,E,F分别是正方形ABCD的边BC,CD上的点,CD上的点,BE=CF,连接AE,BF,将△ABE绕正方形的对角线的交点O按顺时针方向旋转到△BCF,则旋转角是( )
 如图,E,F分别是正方形ABCD的边BC,CD上的点,CD上的点,BE=CF,连接AE,BF,将△ABE绕正方形的对角线的交点O按顺时针方向旋转到△BCF,则旋转角是( )
如图,E,F分别是正方形ABCD的边BC,CD上的点,CD上的点,BE=CF,连接AE,BF,将△ABE绕正方形的对角线的交点O按顺时针方向旋转到△BCF,则旋转角是( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
11.下列运算中正确的是( )
| A. | (a-b)2=a2-b2 | B. | (-a+1)(-a-1)=a2-1 | C. | (-$\frac{1}{2}$)-2=1 | D. | -(-2ab2)2=4a2b4 |
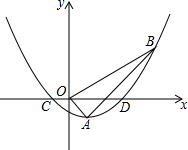 如图,在平面直角坐标系中,顶点为A(1,-1)的抛物线经过点B(5,3),且与x轴交于C,D两点(点C在点D的左侧).
如图,在平面直角坐标系中,顶点为A(1,-1)的抛物线经过点B(5,3),且与x轴交于C,D两点(点C在点D的左侧).
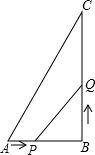 如图所示,在△ABC中∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,点Q从点B开始沿BC边向点C以2cm/s的速度运动.
如图所示,在△ABC中∠B=90°,AB=6cm,BC=8cm,点P从点A开始沿AB边向点B以1cm/s的速度运动,点Q从点B开始沿BC边向点C以2cm/s的速度运动.