题目内容

17．某学习小组的同学做摸球实验时，在一个暗箱里放了多个只有颜色不同的小球，将小球搅匀后任意摸出一个，记下颜色并放回暗箱，再次将球搅匀后任意摸出一个，不断重复．下表是实验过程中记录的数据：
摸球的次数m3004005008001000
摸到白球的次数n186242296483599
摸到白球的频率$\frac{n}{m}$0.6200.6050.5920.6040.599
请估计从暗箱中任意摸出一个球是白球的概率是0.6．

分析 根据表格中的数据，随着实验次数的增大，频率逐渐稳定在0.6左右，即为摸出黄球的概率．

解答 解：观察表格得：通过多次摸球实验后发现其中摸到黄球的频率稳定在0.6左右，
则P白球=0.6．
故答案为：0.6．

点评 此题考查了利用频率估计概率，在同样条件下，大量反复试验时，随机事件发生的频率逐渐稳定在概率附近．

练习册系列答案
相关题目
7．（1）计算下列各题
①a+2b+3a-2b
②2（x2y-3xy2）-3（x2y-4xy2）
（2）先化简，再求值：
（2a2-5a）-$\frac{1}{2}$（2a2-4a+2），其中a=$\frac{1}{3}$．
8．如图，某校要建一个矩形花圃，花圃一边利用长为12m的墙，另外三边用25m长的篱笆围成，并在一边留一个1m宽的门，花圃面积为80m2，设与墙垂直的一边长为xm，则下列关于x的方程正确的是（　　）
A．x（26-2x）=80B．x（24-2x）=80C．（x-1）（26-2x）=80D．x（25-2x）=80
5．若（a-2）2+|b+3|=0，则（a+b）2017=-1．
12．①分解因式：-3a+12a2-12a3；
②利用分解因式计算：已知x+y=4，xy=3，求代数式x2y+xy2的值．
2．设函数y=$\frac{1}{x}$与y=2x+1的图象的交点坐标为（a，b），求$\frac{1}{a}$-$\frac{2}{b}$的值．
9．一次函数y=-3x+5图象上有两点A（$\frac{2}{3}$，y1）、B（2，y2），则y1与y2的大小关系是（　　）
A．y1＞y2B．y1＜y2C．y1=y2D．y1≤y2
6．阅读下面的文字，解答问题：
大家知道$\sqrt{2}$是无理数，而无理数是无限不循环小数，因此$\sqrt{2}$的小数部分我们不可能全部地写出来，于是小明用$\sqrt{2}$-1来表示$\sqrt{2}$的小数部分，你同意小明的表示方法吗？
事实上，小明的表示方法是有道理的，因为$\sqrt{2}$的整数部分是1，将这个数减去其整数部分，差就是小数部分．又例如：∵$\sqrt{4}$＜$\sqrt{7}$＜$\sqrt{9}$，即2＜$\sqrt{7}$＜3，∴$\sqrt{7}$的整数部分为2，小数部分为（$\sqrt{7}$-2）．
根据以上提示回答下列问题：
（1）如果$\sqrt{5}$的小数部分为a，$\sqrt{13}$的整数部分为b，求（a-b）2-b（a+1）的立方根；
（2）若-$\sqrt{5}$=x+y，其中x是整数，且0＜y＜1，求x、y的值；
（3）在（1）（2）的条件下求（x-a）（1-b+y）的值．
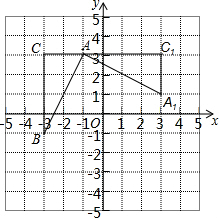10．如图，在平面直角坐标系中，有一Rt△ABC，且点A（-1，3），B（-3，-1），C（-3，3），已知△A1AC1是由△ABC旋转得到的．
（1）旋转中心的坐标是O（0，0），旋转角的度数是90°．
（2）以（1）中的旋转中心为中心，分别画出△A1AC1顺时针旋转90°，180°的三角形．
（3）利用变换前后所形成的图案，可以证明的定理是勾股定理．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网