题目内容
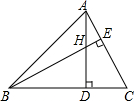 如图,在△ABC中,∠ABC=45°,AC=8,H是高AD和BE的交点,则线段BH的长度为
如图,在△ABC中,∠ABC=45°,AC=8,H是高AD和BE的交点,则线段BH的长度为考点:全等三角形的判定与性质
专题:
分析:根据∠ABC=45°和AD⊥BD可求得AD=BD,易证∠CAD=∠CBE,即可证明△BDH≌△ADC,根据全等三角形对应边相等的性质即可解题.
解答:解:∵∠ABC=45°,AD⊥BD,
∴∠BAD=∠ABD=45°,
∴AD=BD,
∵∠CAD+∠C=90°,∠CBE+∠C=90°,
∴∠CAD=∠CBE,
在△BDH和△ADC中,
,
∴△BDH≌△ADC(ASA),
∴BH=AC=8.
故答案为:8.
∴∠BAD=∠ABD=45°,
∴AD=BD,
∵∠CAD+∠C=90°,∠CBE+∠C=90°,
∴∠CAD=∠CBE,
在△BDH和△ADC中,
|
∴△BDH≌△ADC(ASA),
∴BH=AC=8.
故答案为:8.
点评:本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△BDH≌△ADC是解题的关键.

练习册系列答案
相关题目
 如图,在七边形ABCDEFG中,∠D=90°,其他六个角彼此相等,且AB=2,EF=FG=2
如图,在七边形ABCDEFG中,∠D=90°,其他六个角彼此相等,且AB=2,EF=FG=2| 2 |
A、26+16
| ||
B、30+15
| ||
C、32+16
| ||
D、15+30
|
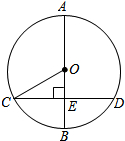 如图,AB是⊙O的直径,弦CD⊥AB于点E,连结OC,若OE=
如图,AB是⊙O的直径,弦CD⊥AB于点E,连结OC,若OE=| 3 |
| 5 |
A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,四边形ABCD是正方形,△ADE经顺时针旋转后与△ABF重合.
如图,四边形ABCD是正方形,△ADE经顺时针旋转后与△ABF重合.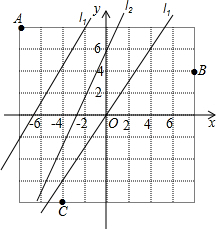 某地区(如图)计划在A,B两城市之间和A,C两城市之间各建一条高速公路.高速公路与其他道路(图中用直线l1,l2,l3表示)交叉处需建立交桥,用坐标表示各立交桥的位置.
某地区(如图)计划在A,B两城市之间和A,C两城市之间各建一条高速公路.高速公路与其他道路(图中用直线l1,l2,l3表示)交叉处需建立交桥,用坐标表示各立交桥的位置.