题目内容
4.已知$\frac{1}{a}$$+\frac{1}{b}$=$\sqrt{5}$(a≠b),则$\frac{a}{b(a-b)}$-$\frac{b}{a(a-b)}$的值为( )| A. | 2$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | 1 |
分析 原式通分并利用同分母分式的减法法则计算,把已知等式变形后代入计算即可求出值.
解答 解:由$\frac{1}{a}$+$\frac{1}{b}$=$\frac{a+b}{ab}$=$\sqrt{5}$,得到a+b=$\sqrt{5}$ab,
则原式=$\frac{{a}^{2}-{b}^{2}}{ab(a-b)}$=$\frac{(a+b)(a-b)}{ab(a-b)}$=$\frac{a+b}{ab}$=$\sqrt{5}$,
故选B.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
12.下列计算正确的是( )
| A. | (a2b)3=a2b3 | B. | (-25xy3)3=-215x3y9 | ||
| C. | m10÷m5($\frac{1}{m}$)5=m10 | D. | x3÷x3=x |
9.下列运算正确的是( )
| A. | a3+a4=a7 | B. | 2a3-3a3=-a3 | C. | (a-1)2=a2-1 | D. | (a+1)(a-1)=a2-2 |
14.$\sqrt{\frac{x}{y}}$是二次根式,则x,y应满足的条件是( )
| A. | x≥0且y≥0 | B. | $\frac{x}{y}$>0 | C. | x≥0且y>0 | D. | $\frac{x}{y}$≥0 |
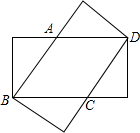 如图,四边形EBGD和四边形BFDH是两个全等的矩形,其中ED、BH交于点A,BG、FD交于点C.
如图,四边形EBGD和四边形BFDH是两个全等的矩形,其中ED、BH交于点A,BG、FD交于点C.