题目内容
16.已知:$\frac{a}{2}$=$\frac{b}{3}$=$\frac{c}{4}$,则$\frac{a+b+c}{a+b-c}$=9.分析 根据比例的性质,可用a表示b、c,根据分式的性质,可得答案.
解答 解:由$\frac{a}{2}$=$\frac{b}{3}$=$\frac{c}{4}$,得
b=$\frac{3a}{2}$,c=2a.
$\frac{a+b+c}{a+b-c}$=$\frac{a+\frac{3a}{2}+2a}{a+\frac{3a}{2}-2a}$=9,
故答案为:9.
点评 本题考查了比例的性质,利用比例的性质用a表示b、c是解题关键.

练习册系列答案
相关题目
7.如果x2-6x+k是完全平方式,则k的值为( )
| A. | ±9 | B. | ±36 | C. | 36 | D. | 9 |
4.已知$\frac{1}{a}$$+\frac{1}{b}$=$\sqrt{5}$(a≠b),则$\frac{a}{b(a-b)}$-$\frac{b}{a(a-b)}$的值为( )
| A. | 2$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | 1 |
11.已知x1、x2是方程x2+3x-1=0的两根,则( )
| A. | x1+x2=-3,x1•x2=-1 | B. | x1+x2=-3,x1•x2=1 | ||
| C. | x1+x2=3,x1•x2=-1 | D. | x1+x2=3,x1•x2=1 |
1.2014年某市初中毕业生约为5.94万人,把5.94万用科学记数表示且保留两个有效数字为( )
| A. | 6.0×104 | B. | 5.9×104 | C. | 59×103 | D. | 6.0万 |
5.菱形ABCD的两条对角线长分别为10和24,求菱形的高( )
| A. | 120 | B. | 240 | C. | $\frac{60}{13}$ | D. | $\frac{120}{13}$ |
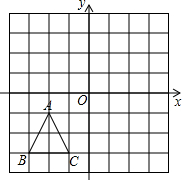 如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3)
如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3)