题目内容
13.在一个不透明的口袋里装有分别标有数字-3、-1、0、2的四个小球,除数字不同外,小球没有任何区别,每次试验先搅拌均匀.从中任取一球,将球上的数字记为a,关于x的一元二次方程ax2-2ax+a+3=0有实数根的概率$\frac{1}{2}$.分析 表示出已知方程根的判别式,根据方程有实数根求出a的范围,即可求出所求概率.
解答 解:∵方程ax2-2ax+a+3=0有实数根,
∴△=4a2-4a(a+3)=-12a≥0,且a≠0,
解得 a<0,
则方程ax2-2ax+a+3=0有实数根的概率$\frac{2}{4}$=$\frac{1}{2}$.
故答案为$\frac{1}{2}$.
点评 此题考查了概率公式,根的判别式,用到的知识点为:
概率=所求情况数与总情况数之比.一元二次方程ax2+bx+c=0(a≠0)的根与△=b2-4ac有如下关系:①当△>0时,方程有两个不相等的两个实数根;②当△=0时,方程有两个相等的两个实数根;③当△<0时,方程无实数根.

练习册系列答案
相关题目
4.已知$\frac{1}{a}$$+\frac{1}{b}$=$\sqrt{5}$(a≠b),则$\frac{a}{b(a-b)}$-$\frac{b}{a(a-b)}$的值为( )
| A. | 2$\sqrt{5}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{5}}{2}$ | D. | 1 |
1.2014年某市初中毕业生约为5.94万人,把5.94万用科学记数表示且保留两个有效数字为( )
| A. | 6.0×104 | B. | 5.9×104 | C. | 59×103 | D. | 6.0万 |
5.菱形ABCD的两条对角线长分别为10和24,求菱形的高( )
| A. | 120 | B. | 240 | C. | $\frac{60}{13}$ | D. | $\frac{120}{13}$ |
2. 如图,若AB∥CD,CD∥EF,则AB与EF的位置关系是( )
如图,若AB∥CD,CD∥EF,则AB与EF的位置关系是( )
 如图,若AB∥CD,CD∥EF,则AB与EF的位置关系是( )
如图,若AB∥CD,CD∥EF,则AB与EF的位置关系是( )| A. | 平行 | B. | 延长后才平行 | C. | 垂直 | D. | 难以确定 |
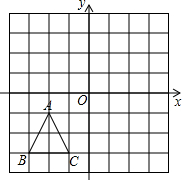 如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3)
如图,已知△ABC三个顶点的坐标分别为A(-2,-1),B(-3,-3),C(-1,-3) 如图,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为6,则反比例函数的表达式是y=-$\frac{6}{x}$.
如图,P是反比例函数图象在第二象限上的一点,且矩形PEOF的面积为6,则反比例函数的表达式是y=-$\frac{6}{x}$.