题目内容
5.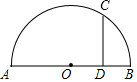 如图,AB是半圆O的直径,点C在半圆O上,CD⊥AB于D,AB=12,DB=4,求CD的长.
如图,AB是半圆O的直径,点C在半圆O上,CD⊥AB于D,AB=12,DB=4,求CD的长.
分析 连接OC,在直角△OCD中利用勾股定理即可求解.
解答  解:连接OC.
解:连接OC.
∵AB是半圆O的直径,
∴OC=OB=$\frac{1}{2}$AB=$\frac{1}{2}$×12=6.
∴OD=OB-DB=6-4=2,
∴在直角△OCD中,CD=$\sqrt{O{C}^{2}-O{D}^{2}}$=$\sqrt{{6}^{2}-{2}^{2}}$=4$\sqrt{2}$.
点评 本题考查了垂径定理和勾股定理,利用垂径定理可以把弦长、半径和弦心距之间的计算转化为直角三角形中边之间的计算.

练习册系列答案
相关题目
15.一次越野赛跑中,当小明跑了1600m时,小刚跑了1450m.此后两人分别以am/s和bm/s匀速跑.又过100s时小刚追上小明,200s时小刚到达终点,300s时小明到达终点.求这次越野赛跑的全程.
(Ⅰ)根据题意,填写下表:
(Ⅱ)求出问题的解.
(Ⅰ)根据题意,填写下表:
| 时间(秒) 路程(米) | 从比赛开始到 匀速跑前 | 从比赛开始到 匀速跑完100秒 | 从比赛开始到 匀速跑完200秒 |
| 小明 | 1600 | 1600+100a | 1600+200a |
| 小刚 | 1450 | 1450+100b | 1450+200b |
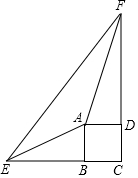 已知四边形ABCD是正方形,E、F分别在CB、CD的延长线上,∠EAF=135°.证明:BE+DF=EF.
已知四边形ABCD是正方形,E、F分别在CB、CD的延长线上,∠EAF=135°.证明:BE+DF=EF.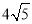 个单位长度的速度沿射线AB方向运动,过点P作PQ⊥AB,交x轴于点Q,PR∥AC交x轴于点R,设点P运动时间为t(秒),线段QR长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);
个单位长度的速度沿射线AB方向运动,过点P作PQ⊥AB,交x轴于点Q,PR∥AC交x轴于点R,设点P运动时间为t(秒),线段QR长为d,求d与t的函数关系式(不要求写出自变量t的取值范围);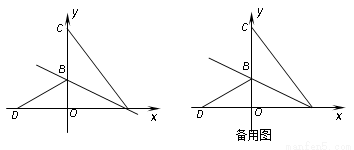
 ;
; .
. B.
B.  C.
C.  D.
D. 