题目内容
1.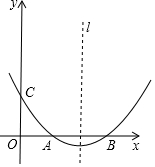 如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-$\frac{2}{3}$),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边)
如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-$\frac{2}{3}$),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边)(1)求抛物线的解析式及A,B两点的坐标;
(2)若(1)中抛物线的对称轴上有点P,使△ABP的面积等于△ABC的面积的2倍,求出点P的坐标;
(3)在(1)中抛物线的对称轴l上是否存在一点Q,使AQ+CQ的值最小?若存在,求AQ+CQ的最小值;若不存在,请说明理由.
分析 (1)因为抛物线的顶点坐标为(4,-$\frac{2}{3}$),所以可以假设抛物线为y=a(x-4)2-$\frac{2}{3}$把点(0,2)代入得到a=$\frac{1}{6}$,令y=0,解方程即可求出A、B两点坐标.
(2)设P(4,m),由题意可得$\frac{1}{2}$•4•|m|=2×$\frac{1}{2}$×4×2,解方程即可.
(3)存在.因为A、B关于对称轴对称,连接CB交对称轴于Q,连接QA,此时QA+QC最短(两点之间线段最短),
解答 解:(1)抛物线的顶点坐标为(4,-$\frac{2}{3}$),可以假设抛物线为y=a(x-4)2-$\frac{2}{3}$把点(0,2)代入得到a=$\frac{1}{6}$,
∴抛物线的解析式为y=$\frac{1}{6}$(x-4)2-$\frac{2}{3}$.
令y=0得到$\frac{1}{6}$(x-4)2-$\frac{2}{3}$=0,解得x=2或6,
∴A(2,0),B(6,0).
(2)设P(4,m),
由题意:$\frac{1}{2}$•4•|m|=2×$\frac{1}{2}$×4×2,解得m=±4,
∴点P坐标(4,4)或(4,-4).
(3)存在.理由如下:
∵A、B关于对称轴对称,连接CB交对称轴于Q,连接QA,此时QA+QC最短(两点之间线段最短),
∴QA+QC的最小值=QA+QC=QB+QC=BC=$\sqrt{{2}^{2}+{3}^{2}}$=$\sqrt{13}$.
点评 本题考查二次函数与x轴的交点、待定系数法.轴对称-最短问题等知识,解题的关键是熟练掌握二次函数的三种形式,灵活运用所学知识解决问题,学会利用对称解决最短问题,属于中常考题型.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
6.将内径为20cm,高为30cm的圆柱形水桶盛满水,全部倒入一个长方体水箱中,水占水箱容积的$\frac{2}{3}$.若水箱的长,宽分别为12cm,9cm,则水箱的高约为多少厘米?(精确到1cm)
13. 如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为( )
如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为( )
 如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为( )
如图,在平面直角坐标系中有一菱形OABC且∠A=120°,点O、B在y轴上,OA=1,现在把菱形向右无滑动翻转,每次翻转60°,点B的落点依次为B1、B2、B3…,连续翻转2017次,则B2017的坐标为( )| A. | (1345,0) | B. | (1345,$\frac{\sqrt{3}}{2}$) | C. | (1345.5,0) | D. | (1345.5,$\frac{\sqrt{3}}{2}$) |
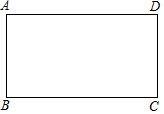 如图,矩形ABCD,点E是边AD上一点,过点E作EF⊥BC,垂足为点F,将△BEF绕着点E逆时针旋转,使点B落在边BC上的点N处,点F落在边DC上的点M处,如果点M恰好是边DC的中点,那么$\frac{AD}{AB}$的值是$\frac{5\sqrt{3}}{6}$.
如图,矩形ABCD,点E是边AD上一点,过点E作EF⊥BC,垂足为点F,将△BEF绕着点E逆时针旋转,使点B落在边BC上的点N处,点F落在边DC上的点M处,如果点M恰好是边DC的中点,那么$\frac{AD}{AB}$的值是$\frac{5\sqrt{3}}{6}$.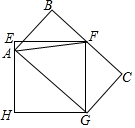 如图,正方形EFGH的边长为6厘米,长方形ABCG的长为8厘米,求CG的长.
如图,正方形EFGH的边长为6厘米,长方形ABCG的长为8厘米,求CG的长. 在一个不透明的袋子中,装有2个红球和1个白球,这些球除了颜色外都相同.如果第一次随机摸出一个小球(不放回),充分搅匀后,第二次再从剩余的两球中随机摸出一个小球,求两次都摸到红球的概率.(用树状图或列表法求解)
在一个不透明的袋子中,装有2个红球和1个白球,这些球除了颜色外都相同.如果第一次随机摸出一个小球(不放回),充分搅匀后,第二次再从剩余的两球中随机摸出一个小球,求两次都摸到红球的概率.(用树状图或列表法求解)
