题目内容
12.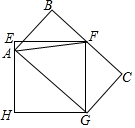 如图,正方形EFGH的边长为6厘米,长方形ABCG的长为8厘米,求CG的长.
如图,正方形EFGH的边长为6厘米,长方形ABCG的长为8厘米,求CG的长.
分析 过F作FP⊥AG于点P,过点A作AQ⊥FG,所以△AFG的面积为:$\frac{1}{2}$AG•FP=$\frac{1}{2}$FG•AQ,从而AG•FP=FG•AQ,利用矩形的性质即可求出FP长度.
解答 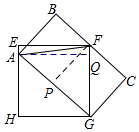 解:过点F作FP⊥AG于点H,过点A作AQ⊥FG于点Q,
解:过点F作FP⊥AG于点H,过点A作AQ⊥FG于点Q,
∴△AFG的面积为:$\frac{1}{2}$AG•FP=$\frac{1}{2}$FG•AQ,
即AG•FP=FG•AQ
∵EF=FG=AQ=6,AG=8,
∴FP=$\frac{9}{2}$
∴CG=FP=$\frac{9}{2}$
点评 本题考查正方形与矩形的性质,解题的关键是根据AG•FP=FG•AQ求出FP的长度,本题属于中等题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 如图,在△AOB中,∠A=30°,∠AOB=90°,双曲线y=$\frac{2}{x}$(x>0)经过点B,双曲线y=$\frac{k}{x}$(x<0)经过点A,则k等于-6.
如图,在△AOB中,∠A=30°,∠AOB=90°,双曲线y=$\frac{2}{x}$(x>0)经过点B,双曲线y=$\frac{k}{x}$(x<0)经过点A,则k等于-6.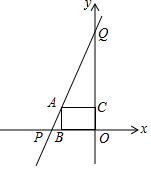 如图,直线y=2x+6与坐标轴分别交于P,Q两点,过函数图象上的点A分别作两坐标轴的垂线,垂足分别为B,C.
如图,直线y=2x+6与坐标轴分别交于P,Q两点,过函数图象上的点A分别作两坐标轴的垂线,垂足分别为B,C.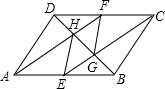 如图,已知在平行四边形ABCD中,点E、F分别是AB、CD的中点,CE、AF与对角线BD分别相交于点G、H,联结EH、FG.
如图,已知在平行四边形ABCD中,点E、F分别是AB、CD的中点,CE、AF与对角线BD分别相交于点G、H,联结EH、FG. 如图是由若干个正方体组成的几何体的俯视图,数字表示该位置上小正方体的个数,则该几何体左视图可能是( )
如图是由若干个正方体组成的几何体的俯视图,数字表示该位置上小正方体的个数,则该几何体左视图可能是( )



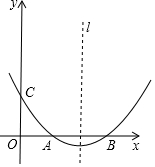 如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-$\frac{2}{3}$),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边)
如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-$\frac{2}{3}$),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边) 如图,四个完全相同的小球上分别写有:0,$\frac{2}{3}$,-5,π四个实数,把它们全部装入一个布袋里,从布袋里任意摸出1个球,球上的数是无理数的概率为$\frac{1}{4}$.
如图,四个完全相同的小球上分别写有:0,$\frac{2}{3}$,-5,π四个实数,把它们全部装入一个布袋里,从布袋里任意摸出1个球,球上的数是无理数的概率为$\frac{1}{4}$.