题目内容
11.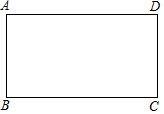 如图,矩形ABCD,点E是边AD上一点,过点E作EF⊥BC,垂足为点F,将△BEF绕着点E逆时针旋转,使点B落在边BC上的点N处,点F落在边DC上的点M处,如果点M恰好是边DC的中点,那么$\frac{AD}{AB}$的值是$\frac{5\sqrt{3}}{6}$.
如图,矩形ABCD,点E是边AD上一点,过点E作EF⊥BC,垂足为点F,将△BEF绕着点E逆时针旋转,使点B落在边BC上的点N处,点F落在边DC上的点M处,如果点M恰好是边DC的中点,那么$\frac{AD}{AB}$的值是$\frac{5\sqrt{3}}{6}$.
分析 根据旋转的性质得到BE=EN,EM=EF,MN=BF,得到BF=FN=NM,推出四边形EFCD是矩形,根据矩形的性质得到EF=CD,由点M恰好是边DC的中点,得到DM=$\frac{1}{2}$CD=$\frac{1}{2}$EM,设CN=x,解直角三角形即可得到结论.
解答 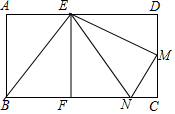 解:如图,将△BEF绕着点E逆时针旋转得到△EMN,
解:如图,将△BEF绕着点E逆时针旋转得到△EMN,
∴BE=EN,EM=EF,MN=BF,
∵EF⊥BC,
∴BF=FN,
∴BF=FN=NM,
∵EF⊥BC,
∴四边形EFCD是矩形,
∴EF=CD,
∵点M恰好是边DC的中点,
∴DM=$\frac{1}{2}$CD=$\frac{1}{2}$EM,
∴∠DEM=30°,
∴∠DME=60°,
∵∠NME=90°,
∴∠CMN=30°,
设CN=x,
∴MN=2x,CM=$\sqrt{3}$x,
∴CD=2$\sqrt{3}$x,
∴BF=FN=NM=2x,
∴BC=5x,
∴$\frac{AD}{AB}$=$\frac{BC}{CD}$,
∴$\frac{AD}{AB}$=$\frac{5\sqrt{3}}{6}$
故答案为:$\frac{5\sqrt{3}}{6}$.
点评 本题考查了旋转的性质,矩形的性质,解直角三角形,正确的作出图形是解题的关键.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
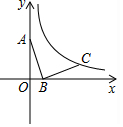 如图,在平面直角坐标系中,点A、B的坐标分贝为(0,3)、(1,0),将线段AB绕点B顺时针旋转90°,得到线段BC,若点C落在函数y=$\frac{k}{x}$(x>0)的图象上,则k的值为( )
如图,在平面直角坐标系中,点A、B的坐标分贝为(0,3)、(1,0),将线段AB绕点B顺时针旋转90°,得到线段BC,若点C落在函数y=$\frac{k}{x}$(x>0)的图象上,则k的值为( )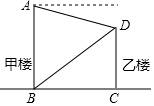 如图,在甲楼的底部B处测得乙楼的顶部D点的仰角为α,在甲楼的顶部A处测得乙楼的顶部D点的俯角为β,如果乙楼的高DC=10米,那么甲楼的高AB=$\frac{10tanβ}{tanα}$+10米(用含α,β的代数式表示)
如图,在甲楼的底部B处测得乙楼的顶部D点的仰角为α,在甲楼的顶部A处测得乙楼的顶部D点的俯角为β,如果乙楼的高DC=10米,那么甲楼的高AB=$\frac{10tanβ}{tanα}$+10米(用含α,β的代数式表示) 如图,在△AOB中,∠A=30°,∠AOB=90°,双曲线y=$\frac{2}{x}$(x>0)经过点B,双曲线y=$\frac{k}{x}$(x<0)经过点A,则k等于-6.
如图,在△AOB中,∠A=30°,∠AOB=90°,双曲线y=$\frac{2}{x}$(x>0)经过点B,双曲线y=$\frac{k}{x}$(x<0)经过点A,则k等于-6.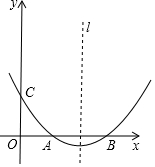 如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-$\frac{2}{3}$),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边)
如图,抛物线y=ax2+bx+c(a≠0)的顶点坐标为(4,-$\frac{2}{3}$),且与y轴交于点C(0,2),与x轴交于A,B两点(点A在点B的左边)