题目内容
 如图,已知点A,D,B,F在一条直线上,△ABC≌△FDE,若MC=4,则EN=
如图,已知点A,D,B,F在一条直线上,△ABC≌△FDE,若MC=4,则EN=考点:全等三角形的性质
专题:
分析:先由△ABC≌△FDE,根据全等三角形对应角相等得出∠A=∠F,∠C=∠E,由内错角相等两直线平行得出AC∥EF,根据两直线平行内错角相等得到∠E=∠AME,等量代换就有∠C=∠AME,于是ME∥CN,又MC∥EN,根据平行四边形定义得出四边形MCNE是平行四边形,于是EN=MC=4.
解答:解:∵△ABC≌△FDE,
∴∠A=∠F,∠C=∠E,
∴AC∥EF,
∴∠E=∠AME,
∴∠C=∠AME,
∴ME∥CN,
又∵MC∥EN,
∴四边形MCNE是平行四边形,
∴EN=MC=4.
故答案为4.
∴∠A=∠F,∠C=∠E,
∴AC∥EF,
∴∠E=∠AME,
∴∠C=∠AME,
∴ME∥CN,
又∵MC∥EN,
∴四边形MCNE是平行四边形,
∴EN=MC=4.
故答案为4.
点评:本题考查了全等三角形的性质,平行线、平行四边形的判定与性质,难度适中.得出ME∥CN是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
已知方程组
,那么x的值是( )
|
| A、1 | B、2 | C、-1 | D、-2 |
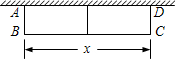 如图,一边利用墙,其余各边用篱笆靠墙围成矩形花圈ABCD,在花圈中间用一道篱笆隔成两个小矩形,墙可利用的最大长度为15m,篱笆总长为24m,设平行于墙的BC边长c m,矩形ABCD的面积为S m2.
如图,一边利用墙,其余各边用篱笆靠墙围成矩形花圈ABCD,在花圈中间用一道篱笆隔成两个小矩形,墙可利用的最大长度为15m,篱笆总长为24m,设平行于墙的BC边长c m,矩形ABCD的面积为S m2.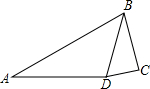 如图,在四边形ABCD中,∠A=30°,∠C=90°,∠ADB=105°,sin∠BDC=
如图,在四边形ABCD中,∠A=30°,∠C=90°,∠ADB=105°,sin∠BDC=