Question

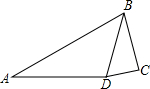如图，在四边形ABCD中，∠A=30°，∠C=90°，∠ADB=105°，sin∠BDC=

3

2

，AD=4．求DC的长．

Answer 1

考点：解直角三角形

专题：

分析：先在Rt△BCD中，由sin∠BDC=

3

2

，得出∠BDC=60°，∠CBD=90°-∠BDC=30°，则∠ADC=∠ADB+∠BDC=165°，根据四边形内角和定理求出∠ABC=360°-∠A-∠ADC-∠C=75°，于是∠ABD=75°-30°=45°．在△ABD中，由正弦定理得出

AD

sin∠ABD

=

BD

sin∠A

，即

4

2 2

=

BD

1 2

，求出BD=2

2

，然后在Rt△BCD中利用30°角所对的直角边等于斜边的一半得出DC=

1

2

BD=

2

．

解答：解：在Rt△BCD中，∵∠C=90°，sin∠BDC=

3

2

，
∴∠BDC=60°，∠CBD=90°-∠BDC=30°，
∴∠ADC=∠ADB+∠BDC=105°+60°=165°，
∴∠ABC=360°-∠A-∠ADC-∠C=75°，
∴∠ABD=75°-30°=45°．
在△ABD中，∵

AD

sin∠ABD

=

BD

sin∠A

，
∴

4

2 2

=

BD

1 2

，
∴BD=2

2

，
∴DC=

1

2

BD=

2

．

点评：本题考查了解直角三角形，特殊角的三角函数值，四边形内角和定理，正弦定理，含30°角的直角三角形的性质，难度适中．求出BD的长是解题的关键．