题目内容
5.如图1在△HGI中,如果O、P分别是GH、GP的中点,那么OP∥HI且OP=$\frac{1}{2}$HI.利用此结论解决如下问题:如图2,已知在矩形ABCD中,M,N分别是边AD,BC的中点,E,F分别是线段BM,CM的中点.(1)求证:△ABM≌△DCM;
(2)判断四边形MENF是什么特殊四边形,并证明你的结论;
(3)当AD:AB=2:1时,四边形MENF是正方形,并加以证明.
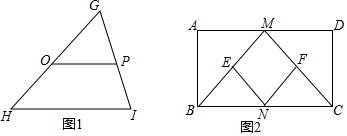
分析 (1)先判断出MA=MD,∠A=∠D=90°,AB=DC即可判断出结论;
(2)先判断出四边形MENF是平行四边形,再判断出ME=MF即可得出结论;
(3)先判断出∠AMB+∠DMC=90°,进而判断出∠AMB=∠ABM=45°,即可得出AB=AM,即可得出结论.
解答 解:(1)∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=DC,
∵M是边AD的中点,
∴MA=MD,
在△ABM和△DCM中,$\left\{\begin{array}{l}{AB=DC}\\{∠A=∠B}\\{MA=MD}\end{array}\right.$,
∴△ABM≌△DCM;
(2)四边形MENF是菱形;
理由:∵N,E,F分别是BC,BM,CM的中点,
∴NE∥CM,NE=$\frac{1}{2}$CM,MF=$\frac{1}{2}$CM,
∴NE=FM,
∵NE∥FM,
∴四边形MENF是平行四边形,
由(1)知,△ABM≌△DCM,
∴BM=CM,
∵E,F分别是BM、CM的中点,
∴ME=$\frac{1}{2}$BM,MF=$\frac{1}{2}$CM,
∴ME=MF,
∴?MENF是菱形;
(3)∵四边形NEMF是正方形,
∴∠EMF=90°,
∴∠AMB+∠DMC=90°,
由(1)知,△ABM≌△DCM,
∴∠AMB=∠DMC,
∴∠AMB=45°,
在△ABM中,∠ABM=90°-45°=45°,
∴AB=AM,
∵M是AD的中点,
∴AD=2AM,
∴AD=2AB,
∴AD:AB=2:1,
故答案为2:1.
点评 此题是四边形综合题,主要考查了矩形的性质,平行四边形的判定和性质,菱形的判定,正方形的性质,全等三角形的判定和性质,解(1)的关键是判断出MA=MD,解(2)的关键是判断出四边形MENF是平行四边形,解(3)的关键是判断出∠AMB=∠ABM=45°.

| A. | 2 | B. | -2 | C. | C、8 | D. | -8 |
| A. | 3 | B. | 2 | C. | 1.5 | D. | 2.5 |
| A. | x2-2x+1=(x-1)2 | B. | (x+1)(x-1)=x2-1 | C. | x2-2x+1=x(x-2)+1 | D. | (x+3)(x-2)=x2+x-6 |
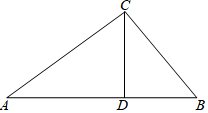 如图,在△ABC中,CD⊥AB于D,AC=20,BC=15,AD=16,
如图,在△ABC中,CD⊥AB于D,AC=20,BC=15,AD=16,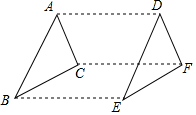 如图,三角形ABC经过平移得到三角形DEF,若∠BAC=65°,则∠EDF=65°.
如图,三角形ABC经过平移得到三角形DEF,若∠BAC=65°,则∠EDF=65°.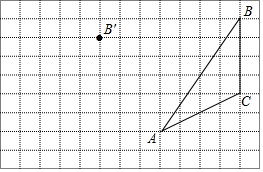 如图,在方格纸内将三角形ABC经过平移后得到三角形A′B′C′,图中标出了点B的对应点B′,解答下列问题.
如图,在方格纸内将三角形ABC经过平移后得到三角形A′B′C′,图中标出了点B的对应点B′,解答下列问题. 某同学想用一块面积为400cm2的正方形纸片,(如图所示)沿着边的方向裁出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2,请你用所学过的知识来说明能否用这块纸片裁出符合要求的纸片.
某同学想用一块面积为400cm2的正方形纸片,(如图所示)沿着边的方向裁出一块面积为300cm2的长方形纸片,使它的长宽之比为3:2,请你用所学过的知识来说明能否用这块纸片裁出符合要求的纸片.