题目内容
16.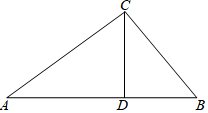 如图,在△ABC中,CD⊥AB于D,AC=20,BC=15,AD=16,
如图,在△ABC中,CD⊥AB于D,AC=20,BC=15,AD=16,(1)求CD的长;
(2)求AB的长.
分析 (1)在直角△ACD中利用勾股定理得出CD的长即可;
(2)利用(1)中所求,在直角△BCD中利用勾股定理求得BD,再根据线段的和差关系求得AB的长.
解答 解:(1)∵CD⊥AB于D,
∴∠ADC=∠BDC=90°.
∵在直角△ACD中,AC=20,AD=16,
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=12;
(2)∵在直角△BCD中,BC=15,CD=12,
∴BD=$\sqrt{B{C}^{2}-C{D}^{2}}$=9,
∴AB=AD+BD=25.
点评 此题主要考查了勾股定理:在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方.正确求出CD的长是解题关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
14.已知正六边形的半径为4,则这个正六边形的面积是( )
| A. | 4 | B. | 24 | C. | 4$\sqrt{3}$ | D. | 24$\sqrt{3}$ |
8.某公司销售一种进价为20元/个的水杯,其销售量y(万个)与销售价格x(元/个)的变化如下表,销售过程中的其他开支(不含成本)总计40万元.
(1)求出该公司销售这种水杯的净利润z(万元)与销售价格x(元/个)的函数关系式,并求出销售价格定为多少时净利润最大?最大值是多少?
(2)该公司要求净利润不低于40万元,请写出销售价格x(元/个)的取值范围.
| 价格x(元/个) | … | 30 | 40 | 50 | 60 | … |
| 销售量y(万个) | … | 5 | 4 | 3 | 2 | … |
(2)该公司要求净利润不低于40万元,请写出销售价格x(元/个)的取值范围.
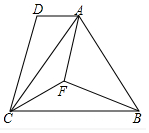 如图,在四边形ABCD中,AB=BC,BF是∠ABC的平分线,连接AB.
如图,在四边形ABCD中,AB=BC,BF是∠ABC的平分线,连接AB. 如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=50°,∠BDC=70°,求∠BED的度数.
如图,BD是△ABC的角平分线,DE∥BC,交AB于点E,∠A=50°,∠BDC=70°,求∠BED的度数.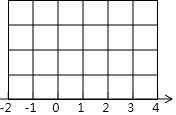 如图,每个小格的顶点叫做格点,每个小正方形边长为1,
如图,每个小格的顶点叫做格点,每个小正方形边长为1,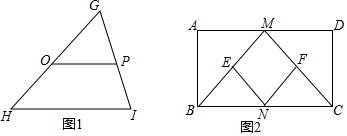
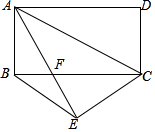 如图,把矩形ABCD沿AC折叠,点D落在点E处,AE交BC于点F,连接BE,若BE:AC=3:5,求AB:BC的值.
如图,把矩形ABCD沿AC折叠,点D落在点E处,AE交BC于点F,连接BE,若BE:AC=3:5,求AB:BC的值.