题目内容
4.下列命题中:(1)形状相同的两个三角形全等;
(2)斜边和一条直角边对应相等的两个直角三角形一定全等;
(3)等腰三角形两腰上的高线相等;
(4)三角形的三条高线交于三角形内一点.
其中真命题的个数有( )
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
分析 根据三角形全等的定义对(1)进行判断;根据直角三角形的判定方法对(2)进行判断;根据等腰三角形的性质对(3)进行判断;根据三角形好线的性质对(4)进行判断.
解答 解:形状、大小相同的两个三角形全等,所以(1)错误;
斜边和一条直角边对应相等的两个直角三角形一定全等,所以(2)正确;
等腰三角形两腰上的高线相等,所以(3)正确;
三角形的三条高线交于一点,所以(4)错误.
故选C.
点评 本题考查了命题与定理:判断一件事情的语句,叫做命题.许多命题都是由题设和结论两部分组成,题设是已知事项,结论是由已知事项推出的事项,一个命题可以写成“如果…那么…”形式. 有些命题的正确性是用推理证实的,这样的真命题叫做定理.也考查了三角形有关性质.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
19.在等腰三角形ABC中,它的两边长分别为8cm和4cm,则它的周长为( )
| A. | 10cm | B. | 12 cm | C. | 20 cm或16 cm | D. | 20 cm |
9.一种细胞每过60分钟便由1个分裂成2个.经过6小时,这种细胞由1个分裂成了多少个?( )
| A. | 32 | B. | 64 | C. | 128 | D. | 16 |
16.当x=1时,下列分式的值为0的是( )
| A. | $\frac{x-1}{{{x^2}-1}}$ | B. | $\frac{x+1}{{{x^2}-1}}$ | C. | $\frac{1-x}{{{x^2}-1}}$ | D. | $\frac{{{x^2}-1}}{x+1}$ |
13.已知⊙O的半径为3,圆心O到直线L的距离为2,则直线L与⊙O的位置关系是( )
| A. | 不能确定 | B. | 相离 | C. | 相切 | D. | 相交 |
14.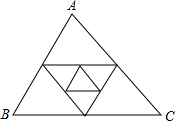 如图,已知△ABC的周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,则第2016个三角形的周长为( )
如图,已知△ABC的周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,则第2016个三角形的周长为( )
 如图,已知△ABC的周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,则第2016个三角形的周长为( )
如图,已知△ABC的周长为1,连结△ABC三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,则第2016个三角形的周长为( )| A. | $\frac{1}{2015}$ | B. | $\frac{1}{2016}$ | C. | $\frac{1}{{2}^{2015}}$ | D. | $\frac{1}{{2}^{2016}}$ |
 如图,在△ABD和△AEC中,AD=AB,AC=AE,∠BAD=∠CAE.求证:DC=BE.
如图,在△ABD和△AEC中,AD=AB,AC=AE,∠BAD=∠CAE.求证:DC=BE. 如图,抛物线y=ax2-4x+c经过坐标原点O,且与x轴交于点A(-4,0)
如图,抛物线y=ax2-4x+c经过坐标原点O,且与x轴交于点A(-4,0) 如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,-1)、B(-1,1)、C(0,-2).
如图,在平面直角坐标系中,△ABC的三个顶点坐标分别为A(-2,-1)、B(-1,1)、C(0,-2).