题目内容
10.某商场将每件进价为20元的玩具以30元的价格出售时,每天可售出300件.经调查当单价每涨1元时,每天少售出10件.若商场想每天获得3750元利润,设每件玩具涨x元,可列方程为:(30+x-20)(300-10x)=3750.对所列方程中出现的代数式,下列说法错误的是( )| A. | (30+x)表示涨价后玩具的单价 | |
| B. | 10x表示涨价后少售出玩具的数量 | |
| C. | (300-10x)表示涨价后销售玩具的数量 | |
| D. | (30+x-20)表示涨价后的每件玩具的单价 |
分析 设涨价x元,然后分别表示出销量和涨价后的单价即可列出方程求解.
解答 解:设涨价x元,根据题意可得:
A、∵(30+x)表示涨价后玩具的单价,∴A选项正确;
B、∵10x表示涨价后少售出玩具的数量,∴B选项正确;
C、∵(300-10x)表示涨价后销售玩具的数量,∴C选项正确;
D、∵(30+x-20)表示涨价后的每件玩具的利润,故D选项错误,
故选D.
点评 本题考查了由实际问题抽象出一元二次方程的知识,解题的关键是能够分别表示出单件利润和总的销售量,从而表示出总利润.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
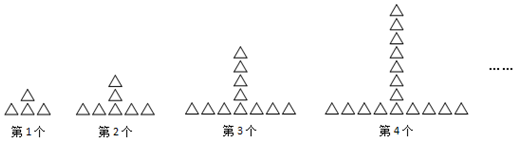
20.如图,每个图形都由同样大小的“△”按照一定的规律组成,其中第1个图形有4个“△”,第2个图形有7个“△”,第3个图形有11个“△”,…,则第8个图形中“△”的个数为( )

| A. | 46 | B. | 48 | C. | 50 | D. | 52 |
1.方程2x-(x+10)=5x+2(x+1)的解是( )
| A. | x=$\frac{4}{3}$ | B. | x=-$\frac{4}{3}$ | C. | x=-2 | D. | x=2 |
18.若m>n,则下列各式正确的是( )
| A. | 2m-2n<0 | B. | m-3>n-3 | C. | -3m>-3n | D. | $\frac{m}{2}$<$\frac{n}{2}$ |
5.一元二次方程2x2-3x+5=0根的情况是( )
| A. | 没有实数根 | B. | 只有一个实数根 | ||
| C. | 有两个相等的实数根 | D. | 有两个不相等的实数根 |
20.二次函数y=ax2+bx+c的部分对应值如表:
则该二次函数y=ax2+bx+c的表达式为y=x2-2x-8.
| x | … | -3 | -2 | 0 | 1 | 3 | 5 | … |
| y | … | 7 | 0 | -8 | -9 | -5 | 7 | … |
 如图,OD=OC,要使△AOD≌△BOC,需添加的一个条件是∠D=∠C(添一个条件即可)
如图,OD=OC,要使△AOD≌△BOC,需添加的一个条件是∠D=∠C(添一个条件即可)