题目内容
在Rt△ABC中，∠C=90°，若AB=2AC，则tanA= ．
考点：特殊角的三角函数值
专题：
分析：根据∠C=90°，可得tanA=
，设AB=2x，AC=x，根据勾股定理求出BC的长度，继而可求解．
| BC |
| AC |
解答：解：在Rt△ABC中，
∵∠C=90°，AB=2AC，
∴设AB=2x，AC=x，
则BC=
=
x，
则tanA=
=
．
故答案为：
．
∵∠C=90°，AB=2AC，
∴设AB=2x，AC=x，
则BC=
| AB2-AC2 |
| 3 |
则tanA=
| BC |
| AC |
| 3 |
故答案为：
| 3 |
点评：本题考查了特殊角的三角函数值，解答本题的关键是根据勾股定理求得另外一边BC的长度．
练习册系列答案
口算能手系列答案
相关题目
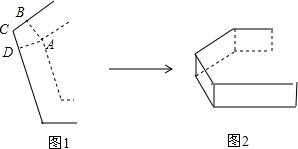将一个正n边形的纸片（如图1）做成一个高相等且底面为正n边形的无盖纸盒，纸盒的各侧面都与底面垂直（如图2），应在正n边形的每个顶点处剪去一个四边形，如图1中的四边形ABCD是其中的一个，则∠BAD=
如图，已知点P是菱形ABCD的边BC上的一点，且∠PAD=∠B=80°，那么∠PDC的度为