题目内容
20.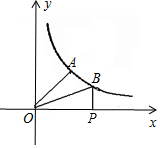 如图,已知A、B是反比例函数y=$\frac{k}{x}$图象上两点,BP⊥x轴,垂足为P.
如图,已知A、B是反比例函数y=$\frac{k}{x}$图象上两点,BP⊥x轴,垂足为P.已知∠AOP=45°,OA=4,tan∠BOP=$\frac{1}{2}$.
(1)求点A的坐标;
(2)连接AB,求四边形AOPB的面积.
分析 (1)过点A作AC⊥OP交OP于点C,在Rt△AOC中,通过解直角三角形即可求出点A的坐标;
(2)由点A的坐标利用待定系数法即可求出反比例函数解析式,在Rt△OBP中,通过解直角三角形可求出点B的坐标,利用分割图形求面积法结合反比例函数系数k的几何意义,即可求出四边形AOPB的面积.
解答 解:(1)过点A作AC⊥OP交OP于点C,如图所示.
在Rt△AOC中,∠AOP=45°,OA=4,
∴AC=OC=2$\sqrt{2}$,
∴点A的坐标为(2$\sqrt{2}$,2$\sqrt{2}$).
(2)把A(2$\sqrt{2}$,2$\sqrt{2}$)代入y=$\frac{k}{x}$,
2$\sqrt{2}$=$\frac{k}{2\sqrt{2}}$,解得:k=8,
∴反比例函数解析式为y=$\frac{8}{x}$.
在Rt△OBP中,tan∠BOP=$\frac{1}{2}$,即OP=2BP,设BP=m,则点B(2m,m),
把B(2m,m)代入y=$\frac{8}{x}$中,
m=$\frac{8}{2m}$,解得:m=2,
∴BP=2,OP=4,
∴S四边形AOPB=S四边形ACPB+S△AOC=$\frac{1}{2}$×(2+2$\sqrt{2}$)×(4-2$\sqrt{2}$)+$\frac{1}{2}$×8=4+2$\sqrt{2}$.
点评 本题考查了反比例函数系数k的几何意义、解直角三角形以及待定系数法求一次函数解析式,解题的关键是:(1)通过解直角三角形找出点A的坐标;(2)利用分割图形求面积法求出四边形AOPB的面积.

练习册系列答案
相关题目
15.某班10名学生校服尺寸与对应人数如下表所示:
则这10名学生校服尺寸的中位数为170cm.
| 尺寸(cm) | 160 | 165 | 170 | 175 | 180 |
| 学生人数(人) | 1 | 3 | 2 | 2 | 2 |
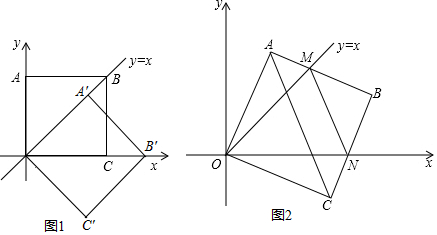
12.如图1~3,在直角边分别为3和4的直角三角形中,每多作一条斜边上的高就增加一个三角形的内切圆,依此类推,图6中有6个直角三角形的内切圆,它们的面积分别记为S1,S2,S3,…,S6,则S1+S2+S3+…+S6的值是( )


| A. | π | B. | $\sqrt{2}$π | C. | 1.6π | D. | $\frac{3}{2}$π |
10.下列运算正确的是( )
| A. | (a+b)2=a2+b2 | B. | (3a2)3=9a6 | C. | 50÷5-2=$\frac{1}{25}$ | D. | $\sqrt{8}$-$\sqrt{50}$=-3$\sqrt{2}$ |
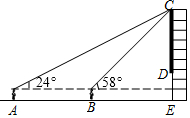 如图是某市中心一家大型购物商城墙面上的电子屏幕,好学的小希想利用所学的知识测量电子屏幕上下端之间的高度,于是她站在屏幕正前方的点A处,测得电子屏幕上端C处的仰角为24°,接着他正对电子屏幕方向前进7m到达点B处,又测得电子屏幕上端C处的仰角为58°,已知图中所有点均在同一平面内,小希的眼睛始终距离地面1.60m,CE⊥AE,DE=3m,请你根据以上测量数据,求该电子屏幕上下端之间的高度CD.(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°≈0.45,sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,结果精确到0.1m)
如图是某市中心一家大型购物商城墙面上的电子屏幕,好学的小希想利用所学的知识测量电子屏幕上下端之间的高度,于是她站在屏幕正前方的点A处,测得电子屏幕上端C处的仰角为24°,接着他正对电子屏幕方向前进7m到达点B处,又测得电子屏幕上端C处的仰角为58°,已知图中所有点均在同一平面内,小希的眼睛始终距离地面1.60m,CE⊥AE,DE=3m,请你根据以上测量数据,求该电子屏幕上下端之间的高度CD.(参考数据:sin24°≈0.41,cos24°≈0.91,tan24°≈0.45,sin58°≈0.85,cos58°≈0.53,tan58°≈1.60,结果精确到0.1m)