题目内容
10．先化简，再求值：$\frac{4}{{x}^{2}-4}$+$\frac{2}{x+2}$-$\frac{1}{x-2}$，其中x=$\sqrt{2}$．分析 先化简题目中的式子，然后将x的值代入即可解答本题．
解答 解：$\frac{4}{{x}^{2}-4}$+$\frac{2}{x+2}$-$\frac{1}{x-2}$
=$\frac{4}{（x+2）（x-2）}+\frac{2}{x+2}-\frac{1}{x-2}$
=$\frac{4+2（x-2）-（x+2）}{（x+2）（x-2）}$
=$\frac{4+2x-4-x-2}{（x+2）（x-2）}$
=$\frac{x-2}{（x+2）（x-2）}$
=$\frac{1}{x+2}$，
当x=$\sqrt{2}$时，原式=$\frac{1}{\sqrt{2}+2}=\frac{2-\sqrt{2}}{2}$．
点评 本题考查分式的化简求值，解答本题的关键是明确分式化简求值的方法．
练习册系列答案
相关题目
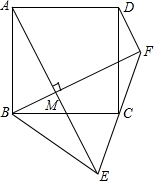正方形ABCD中，点C为线段EF的中点，连接AE、BF交于M，当AE⊥BF，∠BFE=45°，BE=10，则DF的长为2$\sqrt{5}$．
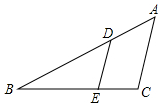如图，△ABC中，点D、E分别在边AB、BC上，DE∥AC，若DB=4，AB=6，BE=3，则EC的长是$\frac{3}{2}$．