题目内容
20.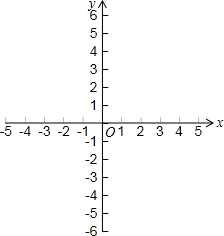 已知抛物线y=x2-2x-3.
已知抛物线y=x2-2x-3.(1)它与y轴的交点的坐标为(0,-3);
(2)在坐标系中利用描点法画出它的图象;
(3)当-1<x<4时,求y的取值范围.
分析 (1)令x=0,求得y,得出与y轴的交点的坐标;
(2)列表,描点,画出函数图象即可;
(3)求得对称轴,以对称轴为分界线,结合图象得出答案即可.
解答 解:(1)当x=0时,y=x2-2x-3=-3,
所以它与y轴的交点的坐标为(0,-3);
(2)列表:
| x | … | -1 | 0 | 1 | 2 | 3 | … |
| y | … | 0 | -3 | -4 | -3 | 0 | … |
 ;
;(3)抛物线y=x2-2x-3的对称轴是x=1,顶点坐标为(1,-4);
当-1<x<1时,-4<y<0;
当1≤x<4时,-4<y<5.
点评 此题考查二次函数的图象与性质,由函数图象确定坐标,图象的交点问题,综合体现了数形结合的思想.

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
11.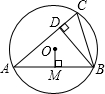 如图,已知⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
如图,已知⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
 如图,已知⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )
如图,已知⊙O的半径为2,锐角△ABC内接于⊙O,BD⊥AC于点D,OM⊥AB于点M,则sin∠CBD的值等于( )| A. | OM的长 | B. | $\frac{1}{2}$OM的长 | C. | 2OM的长 | D. | CD的长 |
15.下列长度的各组线段,能组成直角三角形的是( )
| A. | 12,15,18 | B. | 12,35,36 | C. | 0.3,0.4,0.5 | D. | 2,3,4 |
 已知:AB∥DE,BC∥EF,D,C在AF上,且AD=CF,求证:BC=EF.
已知:AB∥DE,BC∥EF,D,C在AF上,且AD=CF,求证:BC=EF.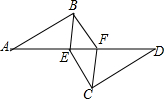 如图,AB∥CD,AB=CD,AE=DF.写出图中全等的三角形△ABE≌△DCF,△ABF≌△DCE,△BEF≌△CFE.
如图,AB∥CD,AB=CD,AE=DF.写出图中全等的三角形△ABE≌△DCF,△ABF≌△DCE,△BEF≌△CFE.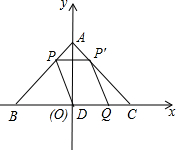 在如图所示的直角坐标系中,若△ABC是等腰直角三角形,AB=AC=8$\sqrt{2}$,D为斜边BC的中点.点P由点A出发沿线段AB做匀速运动,P′是P关于AD的对称点;点Q由点D出发沿射线DC方向做匀速运动,且满足四边形QDPP′是平行四边形.设平行四边形QDPP′的面积为S,DQ=m.
在如图所示的直角坐标系中,若△ABC是等腰直角三角形,AB=AC=8$\sqrt{2}$,D为斜边BC的中点.点P由点A出发沿线段AB做匀速运动,P′是P关于AD的对称点;点Q由点D出发沿射线DC方向做匀速运动,且满足四边形QDPP′是平行四边形.设平行四边形QDPP′的面积为S,DQ=m.