题目内容
7.我国是水资源比较贫乏的国家之一,各地采用了价格调控等手段来达到节约用水的目的,某市用水收费的方法是:水费=基本费+超额费+定额损耗费.若每月用水量不超过最低限量a立方米时,只付基本费8元和每月的定额损耗费c元;若用水量超过a立方米时,除了付同上的基本费和定额损耗费外,超过部分每立方米付b元的超额费.已知每户每月的定额费不超过5元.(1)当月用水量为x立方米时,支付费用为y元,写出y关于x的函数关系式;
(2)该市一家庭今年一季度的用水量和支付费用见下表,根据表中数据求a、b、c.
月份 | 用水量(m3) | 水费(元) |
| 1 | 9 | 9 |
| 2 | 15 | 19 |
| 3 | 22 | 33 |
分析 (1)根据水费=基本费+超额费+定额损耗费,分两种情况列出y关于x的函数关系式;
(2)已知每户每月的定额损耗费不超过5元.由表知第二、第三月份的水费均大于13元,此时满足x>a的函数,于是将(15,19)(22,33)代入即可求出a,b,c的值.
解答 解:月用水量为x立方米,支付费用为y元,则有:
y=$\left\{\begin{array}{l}{8+c(0≤x≤a)}\\{8+b(x-a)+c(x>a)}\end{array}\right.$;
(2)由表知第二、第三月份的水费均大于13元,
故用水量15m3,22m3均大于最低限量am3,
于是就有 $\left\{\begin{array}{l}{19=8+b(15-a)+c}\\{33=8+b(22-a)+c}\end{array}\right.$,
解得b=2,从而2a=c+19,
再考虑一月份的用水量是否超过最低限量am3,
不妨设9>a,将x=9代入x>a的关系式,
得9=8+2(9-a)+c,即2a=c+17,
这与2a=c+19矛盾.
∴9≤a.
从而可知一月份的付款方式应选0≤x≤a的关系式,
因此就有8+c=9,解得c=1.
故a=10,b=2,c=1.
点评 此题主要考查了一次函数的应用以及待定系数法,其解题步骤一般为:①根据函数类型设出函数的解析式(其中系数待定);②根据题意构造关于系数的方程(组);③解方程(组)确定各系数的值;④将求出的系数值代入求出函数的解析式.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
12.建立下列各问题中的方程模型:
(1)某种篮球打八折后每个篮球售价为80元,问该篮球原价为多少?
(2)某厂今年平均每月生产某型号机器170台,比去年月平均产量的1.5倍少10台,求去年的月平均产量.
(1)某种篮球打八折后每个篮球售价为80元,问该篮球原价为多少?
(2)某厂今年平均每月生产某型号机器170台,比去年月平均产量的1.5倍少10台,求去年的月平均产量.
2. 如图所示是一个立体图形的三视图,该物体是( )
如图所示是一个立体图形的三视图,该物体是( )
 如图所示是一个立体图形的三视图,该物体是( )
如图所示是一个立体图形的三视图,该物体是( )| A. |  | B. |  | C. |  | D. |  |
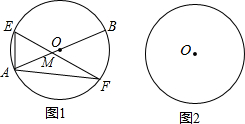 已知AB为⊙O的直径,弦EF所在的直线与直径AB交于点M
已知AB为⊙O的直径,弦EF所在的直线与直径AB交于点M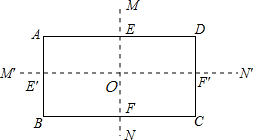 如图,MN、M′N′都是长方形的对称轴,回答下列问题:
如图,MN、M′N′都是长方形的对称轴,回答下列问题: