题目内容

16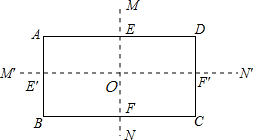．如图，MN、M′N′都是长方形的对称轴，回答下列问题：
（1）请你从图中至少找出3组相等的线段，并说明理由；
（2）若长方形的面积为16，则长方形AE′OE的面积是多少？为什么？

分析 （1）根据轴对称的性质，即可解答；
（2）长方形AE′OE的面积是4，根据轴对称的性质，即可解答．

解答 解：（1）AE=DE，AE′=DF′，BF=CF；
（2）长方形AE′OE的面积是4；
∵MN是对称轴，
∴长方形ABFE与长方形DCFE重合，
∵M′N′对称轴，
∴长方形AE′OE与长方形BE′OF重合，DEOF′与CFOF′重合，
∴四个小长方形的面积都相等，都是大长方形面积的$\frac{1}{4}$×16=4，
即长方形AE′OE的面积是4．

点评 本题考查了轴对称的性质，解决本题的关键是熟记轴对称的性质．

练习册系列答案
相关题目
1．当x=±3时，$\sqrt{{x}^{2}-9}$有最小值，最小值是0．
7．我国是水资源比较贫乏的国家之一，各地采用了价格调控等手段来达到节约用水的目的，某市用水收费的方法是：水费=基本费+超额费+定额损耗费．若每月用水量不超过最低限量a立方米时，只付基本费8元和每月的定额损耗费c元；若用水量超过a立方米时，除了付同上的基本费和定额损耗费外，超过部分每立方米付b元的超额费．已知每户每月的定额费不超过5元．
（1）当月用水量为x立方米时，支付费用为y元，写出y关于x的函数关系式；
（2）该市一家庭今年一季度的用水量和支付费用见下表，根据表中数据求a、b、c．

月份		用水量（m3）
水费（元）
199
21519
32233
4．阅读材料：若a，b都是非负实数，则a+b≥2$\sqrt{ab}$．当且仅当a=b时，“=”成立．
证明：∵（$\sqrt{a}$-$\sqrt{b}$）2≥0，∴a-2$\sqrt{ab}$+b≥0，∴a+b≥2$\sqrt{ab}$．当且仅当a=b时，“=”成立．
举例应用：已知x＞0，求函数y=2x+$\frac{2}{x}$的最小值．
解：y=2x+$\frac{2}{x}$≥2$\sqrt{2x•\frac{2}{x}}$=4，当且仅当2x=$\frac{2}{x}$，即2x2=2，当x=1时，y有最小值为4．
问题解决：汽车的经济时速是指汽车最省油的行驶速度．某种跑车在每小时90～150公里之间行驶时（含90公里和150公里），每公里耗油（$\frac{1}{21}$+$\frac{525}{{x}^{2}}$）升．若该汽车以每小时x公里的速度匀速行驶，1小时的耗油量为y升．
（1）求y关于x的函数关系式；
（2）利用上述阅读材料，求该跑车的经济时速，并求当跑车以经济时速行驶时，每百公里的耗油量（升）（结果保留小数点后一位）．
11．已知$\sqrt{（2a+1）^{2}}$=2a+1，那么a的取值范围是a≥-$\frac{1}{2}$．
1．有六张不透明的卡片，正面的数分别为3.1，$\frac{7}{3}$，$\sqrt{\frac{1}{4}}$，π，$\sqrt{6}$，3.$\stackrel{••}{12}$，除正面的数不同外，其余都相同，将它们背面朝上洗匀后，从中随机抽取一张卡片，抽到写有无理数卡片的概率为（　　）
A．$\frac{1}{6}$B．$\frac{1}{3}$C．$\frac{2}{3}$D．$\frac{5}{6}$
8．袋子里有20个红球，5个白球．每个球除颜色外都相同．
（1）从中任意摸出一个球，摸到白球的概率是多少？
（2）如果第一次摸出一个红球，再从剩下的球中摸出一个，摸到红球的概率是多少？
5．如图，函数y=2x和y=ax+4的图象相交于点A（1，2），则不等式2x≥ax+4的解集为（　　）
A．x≥1B．x≤3C．x≤1D．x≥3
6．为了解某区九年级学生学业考试体育成绩，现从中随机抽取部分学生的体育成绩进行分段（A：40分； B：39-35分； C：34-30分； D：29-20分；E：19-0分）统计如下：
学业考试体育成绩（分数段）统计表
分数段人数（人）频率
A480.2
Ba0.25
C84b
D360.15
E120.05
根据上面提供的信息，回答下列问题：
（1）在统计表中，a的值为60，b的值为0.15，并将统计图补充完整；
（2）甲同学说：“我的体育成绩是此次抽样调查所得数据的中位数．”请问：甲同学的体育成绩应在什么分数段内？C（填相应分数段的字母）
（3）如果把成绩在30分以上（含30分）定为优秀，那么该区今年2400名九年级学生中体育成绩为优秀的学生人数有多少名？

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网