题目内容
15.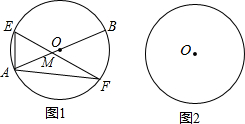 已知AB为⊙O的直径,弦EF所在的直线与直径AB交于点M
已知AB为⊙O的直径,弦EF所在的直线与直径AB交于点M(1)如图1,若M在⊙O内,写出∠AEF与∠BAF的数量关系,并证明;
(2)如图2,若M在⊙O外,写出∠AEF与∠BAF的数量关系,并证明.
分析 (1)连接BF,根据圆周角定理得∠ABF=∠AEF,∠AFB=90°,进而即可求得∠AEF+∠BAF=∠ABF+∠BAF=90°;
(2)连接BE,根据圆周角定理得∠BEF=∠BAF,∠AEB=90°,即可求得∠AEF-∠BAF=90°.
解答 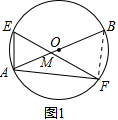 证明:(1)如图1所示;连接BF,
证明:(1)如图1所示;连接BF,
则∠ABF=∠AEF,
∵AB是直径,
∴∠AFB=90°,
∴∠AEF+∠BAF=∠ABF+∠BAF=90°;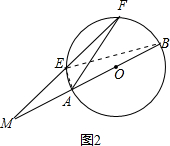 (2)如图2所示,连接BE,
(2)如图2所示,连接BE,
则∠BEF=∠BAF,
∵AB是直径,
∴∠AEB=90°,
∴∠AEF=∠AEB+∠BEF=∠AEB+∠BAF=90°+∠BAF,
即∠AEF-∠BAF=90°.
点评 本题考查了圆周角定理,作出辅助线构建相等的圆周角是解题的关键.

练习册系列答案
相关题目
3. 下面四个所给的选项中,能折成如图给定的图形的是( )
下面四个所给的选项中,能折成如图给定的图形的是( )
 下面四个所给的选项中,能折成如图给定的图形的是( )
下面四个所给的选项中,能折成如图给定的图形的是( )| A. |  | B. |  | C. |  | D. |  |
7.我国是水资源比较贫乏的国家之一,各地采用了价格调控等手段来达到节约用水的目的,某市用水收费的方法是:水费=基本费+超额费+定额损耗费.若每月用水量不超过最低限量a立方米时,只付基本费8元和每月的定额损耗费c元;若用水量超过a立方米时,除了付同上的基本费和定额损耗费外,超过部分每立方米付b元的超额费.已知每户每月的定额费不超过5元.
(1)当月用水量为x立方米时,支付费用为y元,写出y关于x的函数关系式;
(2)该市一家庭今年一季度的用水量和支付费用见下表,根据表中数据求a、b、c.
(1)当月用水量为x立方米时,支付费用为y元,写出y关于x的函数关系式;
(2)该市一家庭今年一季度的用水量和支付费用见下表,根据表中数据求a、b、c.
月份 | 用水量(m3) | 水费(元) |
| 1 | 9 | 9 |
| 2 | 15 | 19 |
| 3 | 22 | 33 |
5. 如图,函数y=2x和y=ax+4的图象相交于点A(1,2),则不等式2x≥ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A(1,2),则不等式2x≥ax+4的解集为( )
 如图,函数y=2x和y=ax+4的图象相交于点A(1,2),则不等式2x≥ax+4的解集为( )
如图,函数y=2x和y=ax+4的图象相交于点A(1,2),则不等式2x≥ax+4的解集为( )| A. | x≥1 | B. | x≤3 | C. | x≤1 | D. | x≥3 |