题目内容
14.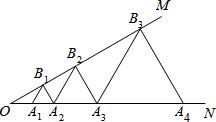 如图,已知,∠MON=30°,点A1,A2,A3在射线ON上,点B1,B2,B3…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形,若OA1=1,则△A4B4A5的边长为8.
如图,已知,∠MON=30°,点A1,A2,A3在射线ON上,点B1,B2,B3…在射线OM上,△A1B1A2,△A2B2A3,△A3B3A4…均为等边三角形,若OA1=1,则△A4B4A5的边长为8.
分析 由等边三角形的性质可证得A2B1⊥OB1,再根据30°角所对的直角边是斜边的一半可求得A2B1=$\frac{1}{2}$OA2,依此类推可求得答案.
解答 解:∵△A1B1A2为等边三角形,
∴∠B1A1A2=60°,
∵∠MON=30°,
∴∠OB1A2=30°+60°=90°,
∴A2B1=$\frac{1}{2}$OA2,
同理可求得:B4A5=$\frac{1}{2}$OA5,
∵OA1=1,
∴OA4=2OA3=4OA2=8OA1=8,OA5=2OA4=4OA3=8OA2=16OA1=16,
∴A4A5=OA5-OA4=16-8=8,
故答案为8.
点评 本题主要考查等边三角形的性质及含30°角的直角三角形的性质,由条件得到OA5=2OA4=4OA3=8OA2=16OA1是解题的关键.

练习册系列答案
 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
相关题目
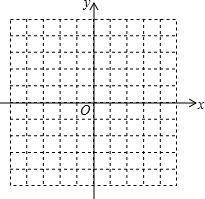 已知在等腰△ABC中,AB=AC,对称轴为x轴,点A的坐标为(-3,0),点B的坐标为(1,3).
已知在等腰△ABC中,AB=AC,对称轴为x轴,点A的坐标为(-3,0),点B的坐标为(1,3).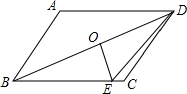 如图,在?ABCD中,O是对角线BD的中点,且AB≠AD,过点O作OE⊥BD于点E,若?ABCD的周长为20,则△CDE的周长为10.
如图,在?ABCD中,O是对角线BD的中点,且AB≠AD,过点O作OE⊥BD于点E,若?ABCD的周长为20,则△CDE的周长为10. 如图,将△ABC沿BC方向平移至△DEF的位置,若BC=5,BF=15
如图,将△ABC沿BC方向平移至△DEF的位置,若BC=5,BF=15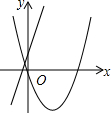
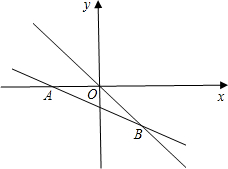 如图,在平面直角坐标系中,直线y=-$\frac{\sqrt{3}}{5}$x-$\frac{3\sqrt{3}}{5}$与x轴交于点A,与直线y=-$\frac{\sqrt{3}}{2}$x交于点B.
如图,在平面直角坐标系中,直线y=-$\frac{\sqrt{3}}{5}$x-$\frac{3\sqrt{3}}{5}$与x轴交于点A,与直线y=-$\frac{\sqrt{3}}{2}$x交于点B.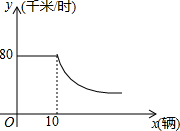 随着私家车的增加,城市的交通也越来越拥挤,通常情况下,某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量x(辆)的关系如图所示,当x≥10时,y与x成反比例函数关系,当车速度低于20千米/时,交通就会拥堵,为避免出现交通拥堵,高架桥上每百米拥有车的数量x应该满足的范围是0<x≤40.
随着私家车的增加,城市的交通也越来越拥挤,通常情况下,某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量x(辆)的关系如图所示,当x≥10时,y与x成反比例函数关系,当车速度低于20千米/时,交通就会拥堵,为避免出现交通拥堵,高架桥上每百米拥有车的数量x应该满足的范围是0<x≤40.