题目内容
12. 已知二次函数y=x2-4x+3.
已知二次函数y=x2-4x+3.(1)求出该函数与x轴的交点坐标、与y轴的交点坐标;
(2)在平面直角坐标系中,用描点法画出该二次函数的图象;
| x | … | … | |||||
| y | … | … |
①当自变量x的取值范围满足什么条件时,y<0?
②当0≤x<3时,y的取值范围是多少?
分析 (1)令y=0得关于x的一元二次方程,求解得到两根,此即为与x轴的两交点坐标;令x=0,求得y的值即可求得与y轴的交点坐标;
(2)通过列表、描点、连线画出函数的图象.
(3)根据图象回答即可.
解答 解:(1)令y=0,得x2-4x+3=0,
解得x1=1,x2=3,
故与x轴的交点坐标:(1,0),(3,0);
令x=0,得y=3,
故与y轴的交点坐标:(0,3);
(2)列表:
| x | 0 | 1 | 2 | 3 | 4 |
| y | 3 | 0 | -1 | 0 | 3 |

(3)①当自变量x的取值范围满足1<x<3 时,y<0;
②当0≤x<3时,y的取值范围是-1≤y≤3.
点评 此题考查了二次函数的图象,利用描点法作二次函数图象,二次函数和不等式的关系,作出函数的图象解题的关键.

练习册系列答案
相关题目
3. 如图,在Rt△ABO中,∠AOB=90°,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线长PQ的最小值是( )
如图,在Rt△ABO中,∠AOB=90°,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线长PQ的最小值是( )
 如图,在Rt△ABO中,∠AOB=90°,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线长PQ的最小值是( )
如图,在Rt△ABO中,∠AOB=90°,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线长PQ的最小值是( )| A. | A$\sqrt{6}$ | B. | $\sqrt{7}$ | C. | 2$\sqrt{2}$ | D. | 3 |
7.抛物线y=-(x+2)2-5的顶点坐标是( )
| A. | (-2,5) | B. | (2,5) | C. | (-2,-5) | D. | (2,-5) |
2.-$\frac{1}{2}$的倒数是( )
| A. | $\frac{1}{2}$ | B. | -2 | C. | 2 | D. | 以上都不对 |

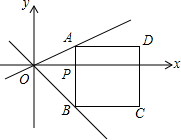 如图,直角坐标系中,点P(t,0)是x轴上的一个动点,过点P作y轴的平行线,分别与直线y=$\frac{1}{2}$x,直线y=-x交于A,B两点,以AB为边向右侧作正方形ABCD.
如图,直角坐标系中,点P(t,0)是x轴上的一个动点,过点P作y轴的平行线,分别与直线y=$\frac{1}{2}$x,直线y=-x交于A,B两点,以AB为边向右侧作正方形ABCD.