题目内容
5.解方程:(1)2(x-3)=3x(x-3);
(2)x2-2x=2x+1.
分析 (1)运用运用因式分解法解一元二次方程;
(2)运用配方法解一元二次方程.
解答 解:(1)2(x-3)=3x(x-3)
移项,得2(x-3)-3x(x-3)=0
整理,得(x-3)(2-3x)=0
∴x-3=0或2-3x=0
解得:x1=3,x2=$\frac{2}{3}$;
(2)原方程化为:x2-4x=1
配方,得x2-4x+4=1+4
整理,得(x-2)2=5
∴x-2=$±\sqrt{5}$,
即x1=2$+\sqrt{5}$,x2=2$-\sqrt{5}$.
点评 本题考查的是一元二次方程的解法,正确运用因式分解法和配方法解一元二次方程是解题的关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
15.某玩具厂在圣诞节期间准备生产A、B两种玩具共80万套,两种玩具的成本和售价如下表:
(1)若该厂所筹集资金为2180万元,且所筹资金全部用于生产,则这两种玩具各生产多少万套?
(2)设该厂生产A种玩具x万套,两种玩具所获得的总利润为w万元,请写出w与x的关系式.
(3)由于资金短缺,该厂所筹集的资金有限,只够生产A种49万套、B种31万套或者A种50万套、B种30万套.但根据市场调查,每套A种玩具的售价将提高a元(a>0),B种玩具售价不变,且所生产的玩具可全部售出,该玩具厂将如何安排生产才能获得最大利润?
| A | B | |
| 成本(元/套) | 25 | 28 |
| 售价(元/套) | 30 | 34 |
(2)设该厂生产A种玩具x万套,两种玩具所获得的总利润为w万元,请写出w与x的关系式.
(3)由于资金短缺,该厂所筹集的资金有限,只够生产A种49万套、B种31万套或者A种50万套、B种30万套.但根据市场调查,每套A种玩具的售价将提高a元(a>0),B种玩具售价不变,且所生产的玩具可全部售出,该玩具厂将如何安排生产才能获得最大利润?
 ,
, ).
).
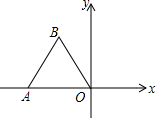 如图,△OAB是边长为2的等边三角形.
如图,△OAB是边长为2的等边三角形.
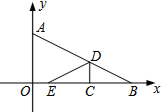 如图,点A(0,2),B(4,0)两点的坐标,将△ABO沿着垂直于x轴的线段CD折叠(点C在x轴上,点D在AB上,点D不与A,B重合),如图,使点E落在x轴上.设点C的坐标为(x,0),△CDE与△ABO重叠部分的面积为S.
如图,点A(0,2),B(4,0)两点的坐标,将△ABO沿着垂直于x轴的线段CD折叠(点C在x轴上,点D在AB上,点D不与A,B重合),如图,使点E落在x轴上.设点C的坐标为(x,0),△CDE与△ABO重叠部分的面积为S.