题目内容
8. 如图所示,过⊙0上一点A作弦AB和直线MN,过点O作OB垂线交AB于点P,交MN点C,若CP=CA,试说明MN是⊙0的切线.
如图所示,过⊙0上一点A作弦AB和直线MN,过点O作OB垂线交AB于点P,交MN点C,若CP=CA,试说明MN是⊙0的切线.
分析 首先连接OA,可得∠OAB=∠B,证得∠OAB+∠OPB=90°,由CP=CA,可得∠APC=∠CAP,等量代换得出∠CAP=∠OPB,得出结论.
解答 解: 连接OA,∵OA=OB,∴∠OAB=∠B,
连接OA,∵OA=OB,∴∠OAB=∠B,
∵OC⊥OB,
∴∠B+∠OPB=90°,
∴∠OAB+∠OPB=90°,
∵CP=CA,
∴∠APC=∠CAP,
∵∠OPB=∠APC,
∴∠CAP=∠OPB,
∴∠OAB+∠CAP=90°,
即OA⊥MN,
所以MN是⊙0的切线.
点评 本题考查了切线的判定定理、等腰三角形的性质、直角三角形的性质、勾股定理,熟练掌握切线的判定是解决此题的关键.

练习册系列答案
相关题目
3. 如图,在Rt△ABO中,∠AOB=90°,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线长PQ的最小值是( )
如图,在Rt△ABO中,∠AOB=90°,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线长PQ的最小值是( )
 如图,在Rt△ABO中,∠AOB=90°,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线长PQ的最小值是( )
如图,在Rt△ABO中,∠AOB=90°,OA=OB=4,⊙O的半径为1,点P是AB边上的动点,过点P作⊙O的一条切线PQ(点Q为切点),则切线长PQ的最小值是( )| A. | A$\sqrt{6}$ | B. | $\sqrt{7}$ | C. | 2$\sqrt{2}$ | D. | 3 |
 的图象向上平移2个单位后,所得图象的函数表达式是___;
的图象向上平移2个单位后,所得图象的函数表达式是___;
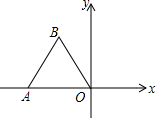 如图,△OAB是边长为2的等边三角形.
如图,△OAB是边长为2的等边三角形.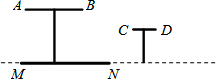
 如图,虚线表示太阳光线.画出标杆AB分别在地面上和墙上的投影的示意图.
如图,虚线表示太阳光线.画出标杆AB分别在地面上和墙上的投影的示意图.