题目内容
9.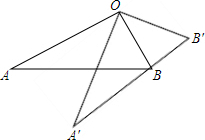 如图,∠AOB=90°,将Rt△OAB绕点O按逆时针方向旋转至Rt△OA′B′,使点B恰好落在边A′B′上.已知tanB=2,OB=5,则BB′=2$\sqrt{5}$.
如图,∠AOB=90°,将Rt△OAB绕点O按逆时针方向旋转至Rt△OA′B′,使点B恰好落在边A′B′上.已知tanB=2,OB=5,则BB′=2$\sqrt{5}$.
分析 根据旋转的性质得出△OAB≌△OA′B′,则有OB=OB′.根据勾股定理,可得B′D的长,根据等腰三角形的性质,可得答案.
解答 解:根据旋转得△OAB≌△OA′B′,
∴OB=OB′,∠ABO=∠B′,
如图,过O作OD⊥BB′,则D为BB′的中点,
∴tanB′=$\frac{OD}{B′D}$=2,
得OD=2B′D.
在Rt△B′OD中,由勾股定理,得
OD2+B′D2=OB′2,
(2B′D)2+B′D2=52.
解得:B′D=$\sqrt{5}$或B°D=-$\sqrt{5}$(不符合题意舍).
由等腰三角形的性质,得BB′=2B′D=2$\sqrt{5}$.
故答案为:2$\sqrt{5}$.
点评 本题考查了旋转的性质,利用了旋转前后的图形全等,利用狗定理得出B′D是解题关键,又利用了全等三角形的性质.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
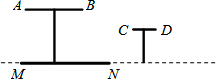
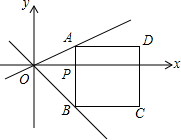 如图,直角坐标系中,点P(t,0)是x轴上的一个动点,过点P作y轴的平行线,分别与直线y=$\frac{1}{2}$x,直线y=-x交于A,B两点,以AB为边向右侧作正方形ABCD.
如图,直角坐标系中,点P(t,0)是x轴上的一个动点,过点P作y轴的平行线,分别与直线y=$\frac{1}{2}$x,直线y=-x交于A,B两点,以AB为边向右侧作正方形ABCD.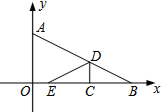 如图,点A(0,2),B(4,0)两点的坐标,将△ABO沿着垂直于x轴的线段CD折叠(点C在x轴上,点D在AB上,点D不与A,B重合),如图,使点E落在x轴上.设点C的坐标为(x,0),△CDE与△ABO重叠部分的面积为S.
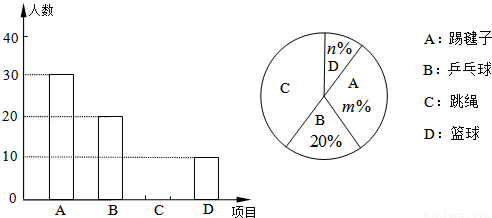
如图,点A(0,2),B(4,0)两点的坐标,将△ABO沿着垂直于x轴的线段CD折叠(点C在x轴上,点D在AB上,点D不与A,B重合),如图,使点E落在x轴上.设点C的坐标为(x,0),△CDE与△ABO重叠部分的面积为S. 如图,虚线表示太阳光线.画出标杆AB分别在地面上和墙上的投影的示意图.
如图,虚线表示太阳光线.画出标杆AB分别在地面上和墙上的投影的示意图.