题目内容

5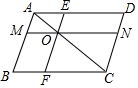．如图，在?ABCD中，点O为对角线AC上的一点，过点O分别作EF∥AB，MN∥AD，则图中面积相等的平行四边形有（　　）
A．4对B．3对C．2对D．1对

分析 由?ABCD的对角线AC上有一点O，过O点作EF∥AB，过P点作MN∥AD，易得四边形AMOE，四边形CNOF，四边形BFOM，四边形ONDE，四边形AMND，四边形BCNM，四边形ABFE，四边形CDEF是平行四边形，即可得S△ABC=S△ADC，S△AOM=S△AOE，S△COF=S△CON，继而可证得S?BFOM=S?ONDGES?ABEF=S?ADNM，S?BCNM=S?CDEF．

解答 解：∵四边形ABCD是平行四边形，
∴AB∥CD，AD∥BC，
∵EF∥AB，MN∥AD，
∴AB∥EF∥CD，AD∥MN∥BC，
∴四边形AMOE，四边形CNPH，四边形BFOM，四边形ONDE，四边形AMND，四边形BCNM，四边形ABFE，四边形CDEF是平行四边形，
∴S△ABC=S△ADC，S△AOM=S△AOG，S△COF=S△CON，
∴S?BFOM=S?ONDE，
∴S?ABEF=S?ADNM，S?BCNM=S?CDEF，
即图中面积相等的平行四边形有3对．
故选B．

点评 此题考查了平行四边形的判定与性质．此题难度适中，注意掌握数形结合思想的应用．

练习册系列答案
相关题目
15．向阳村2013年的人均收入为10000元，2015年人均收入为12100元，若2013年到2015年人均收入的年平均增长率相同．
（1）求人均收入的年平均增长率；
（2）2014年的人均收入是多少元？
16．已知函数 y=kx（k≠0）、y=$\frac{k}{x}$（k≠0），它们在同一直角坐标系内的大致图象可能是（　　）
A．B．C．D．
13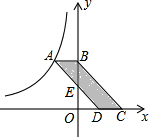．如图，?ABCD的顶点A在反比例函数图象上，边CD落在x轴上，点B在y轴上，AD交y轴于点E，OE：EB=1：2，四边形BCDE的面积为6，则这个反比例函数的解析式是（　　）
A．$y=-\frac{7}{x}$B．$y=-\frac{8}{x}$C．$y=-\frac{9}{x}$D．$y=-\frac{10}{x}$
20．方程$\frac{x-1}{x-2}+\frac{2}{2-x}=2$的解是（　　）
A．x=1B．x=-1C．x=2D．x=-2
10．小明在做解方程作业时，不小心将方程中的一个常数污染了看不清楚，被污染的方程式2y-$\frac{1}{2}$=$\frac{1}{2}$y+，怎么办呢？小明想了想便翻看书后的答案，得知此方程的解是y=$\frac{7}{3}$，于是很快补好这个常数，这个常数应是（　　）
A．1B．-2C．3D．4
17．设m，n是方程x2-x-2015=0的两个不相等的实数根，则m2+n的值是（　　）
A．2014B．2015C．2016D．2017
6．如图，作∠α的补角，然后再画补角的平分线．（不写作法，保留作图痕迹）
7．如果|a+2|+|b-1|=0，那么（a+b）的值是（　　）
A．-2B．2C．-1D．1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网