题目内容
解方程组:
.
|
考点:高次方程
专题:计算题
分析:两个方程相加消掉未知数x,然后去掉分母得到关于y的一元二次方程,求出y的值,再代入第二个方程求出x的值,即可得解.
解答:解:
,
①+②得,
+
+2=3,
两边都乘以(2y-1)(y+1),去分母得,
2y(y+1)+2y-1=(2y-1)(y+1),
2y2+2y+2y-1=2y2+y-1,
解得y=0,
把y=0代入②得,
+1=1,
解得x=1,
经检验,x=1,y=0是方程组的解,
所以,方程组的解是
.
|
①+②得,
| 2y |
| 2y-1 |
| 1 |
| y+1 |
两边都乘以(2y-1)(y+1),去分母得,
2y(y+1)+2y-1=(2y-1)(y+1),
2y2+2y+2y-1=2y2+y-1,
解得y=0,
把y=0代入②得,
| x-1 |
| x |
解得x=1,
经检验,x=1,y=0是方程组的解,
所以,方程组的解是
|
点评:本题考查了解高次方程,观察方程的特点,两个方程相加消掉未知数x是解题的关键.

练习册系列答案
 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
“顺风”汽车队车辆数是“速达”汽车队车辆数的2倍,现从“顺风”队调9辆去“速达”队后,“顺风”队汽车数是“速达”队汽车数的1.5倍,求“顺风”和“速达”两队原来各有汽车多少辆?若设“速达”队原来有汽车x辆,根据题意,得( )
| A、2x-9=1.5(x+9) |
| B、2x=1.5x+9 |
| C、x-9=1.5x+9 |
| D、2x-9=-1.5x |
 双曲线y=
双曲线y=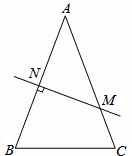 如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.
如图,在△ABC中,AB=AC,AB的垂直平分线交AB于N,交AC于M.
 如图,某渔船向正东方向以10海里/时的速度航行,在A处测得岛C在北偏东的60°方向,1时后前进到B处,测得岛C在北偏东30°方向,已知该岛周围9海里内有暗礁.
如图,某渔船向正东方向以10海里/时的速度航行,在A处测得岛C在北偏东的60°方向,1时后前进到B处,测得岛C在北偏东30°方向,已知该岛周围9海里内有暗礁.