Question

13．如图，在正方形ABCD的边的折线B-C-D上取一点P，P不与B、C、D三点重合，作直线AP，点B关于直线AP的对称点为E，连接BE，DE，直线DE交直线AP于点F．
（1）如图1，若P在线段BC上，依题意补全图1；
（2）如图1，若∠PAB=25°，求∠ADF的度数；
（3）如图2，若P在线段CD上，请用等式丧示线段AD，DF，EF之间的数量关系，并证明．

Answer 1

分析 （1）根据题意画出图形即可．
（2）只要证明AE=AD，求出∠DAE，根据∠ADF=$\frac{1}{2}$（180°-∠DAE）计算即可．
（3）结论：2AD²=EF²+DF²．只要证明△BDF是直角三角形即可解决问题．

解答 解：（1）补全的图如图1所示，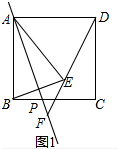


（2）∵四边形ABCD是正方形，
∴AB=AD，∠BAD=90°，
∵AB=AE，
∴AE=AD，
∵∠PAB=∠PAE=22.5°，
∴∠DAE=90°-∠BAE=90°-45°=45°，
∴∠ADE=∠AED=$\frac{1}{2}$（180°-∠DAE）=67.5°．

（3）结论：2AD²=EF²+DF²．
理由：如图2中，连接BF、BD，BF与CD交于点K．

∵E、B关于AF对称，
∴∠ABF=∠AEF，EF=BF，
∵AE=AB=AD，
∴∠AEF=∠ADE=∠ABF，
∵∠ADC=∠ABC=∠C=90°，
∴∠CDF+∠ADE=90°，∠CBF+∠ABF=90°，
∴∠CBF=∠CDF，
∵∠CKB=∠DKF，
∴∠DFK=∠C=90°，
在Rt△DBF中，BD²=BF²+DF²，
∵DB²=2AD²，
∴2AD²=EF²+DF²．

点评 本题考查正方形的性质、对称的性质、勾股定理等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，属于中考常考题型．