题目内容
2.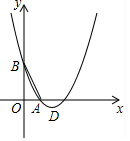 如图,已知抛物线y1=x2+bx+c经过A(1,0),B(0,2)两点,顶点为D.
如图,已知抛物线y1=x2+bx+c经过A(1,0),B(0,2)两点,顶点为D.(1)分别求抛物线y1=x2+bx+c和直线AB:y2=kx+m(k≠0)的解析式;
(2)请根据图象直接写出:二次函数y1=x2+bx+c的值大于一次函数y2=kx+m的值时x的取值范围;
(3)将△OAB绕点A顺时针旋转90°后,点B落到点C的位置,将抛物线沿y轴平移后经过点C,求平移后所得图象的函数关系式.
分析 (1)把点A、B的坐标分别代入抛物线解析式、直线解析式,求得系数即可;
(2)结合函数图象可以直接得到答案;
(3)根据旋转的知识可得:A(1,0),B(0,2),由OA=1,OB=2,可得旋转后C点的坐标为(3,1),可知抛物线y=x2-3x+b过点(3,1),故可知将原抛物线沿y轴向下平移1个单位后过点C.于是得到平移后的抛物线解析式.
解答  解:(1)把A(1,0),B(0,2)代入y1=x2+bx+c,得
解:(1)把A(1,0),B(0,2)代入y1=x2+bx+c,得
$\left\{\begin{array}{l}{1+b+c=0}\\{c=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=-3}\\{c=2}\end{array}\right.$,
则该抛物线解析式是:y=x2-3x+2.
把A(1,0),B(0,2)代入y2=kx+m(k≠0),得
$\left\{\begin{array}{l}{k+m=0}\\{m=2}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{m=2}\end{array}\right.$,
则该直线的解析式是y=-2x+2;
(2)由图象得到:当x<0或x>1时,二次函数y1=x2+bx+c的值大于一次函数y2=kx+m的值.
(3)设抛物线沿y轴平移后的抛物线为y=x2-3x+b.
由(1)知,抛物线解析式是:y=x2-3x+2.
∵A(1,0),B(0,2),
∴OA=1,OB=2,
可得旋转后C点的坐标为(3,1),
将其代入y=x2-3x+b,
即1=32-3×3+b,
解得b=1,
∴将原抛物线沿y轴向下平移1个单位后过点C.
∴平移后的抛物线解析式为:y=x2-3x+1.
点评 本题主要考查待定系数法求二次函数的解析式和二次函数的图象的变换的知识点,熟练掌握图象变换等知识是解答本题的关键,此题很容易结合一次函数出现在综合题中,需要同学们注意.

 如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,则图中与∠EAD相等的角(不包括∠EAD)有( )
如图,AD是△ABC的外角∠EAC的平分线,与△ABC的外接圆交于点D,则图中与∠EAD相等的角(不包括∠EAD)有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
| A. | ±1 | B. | ±2 | C. | -2或0 | D. | 0或2 |
| A. | ∠A=∠B-∠C | B. | ∠A:∠B:∠C=1:3:4 | C. | $a:b:c=1:\sqrt{2}:3$ | D. | a2+c2=b2 |
| A. | -(x-y)=-x-y | B. | 若3x=4y,则3x+5m=4y+5m | ||
| C. | 若am2=bm2,则a=b | D. | 1÷($\frac{1}{3}$-$\frac{1}{2}$)=1÷$\frac{1}{3}$-1÷$\frac{1}{2}$=3-2=1 |
| A. | -25ab2 | B. | 25a2b2 | C. | -25a2b2 | D. | 25a2b |
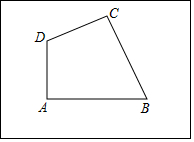 小亮家的房前有一块矩形的空地,空地上有四棵银杏树A、B、C,D,且∠A=∠C=90°,小亮想建一个圆形花坛,使四棵树都在花坛的边上.小亮请小明帮他设计方案:
小亮家的房前有一块矩形的空地,空地上有四棵银杏树A、B、C,D,且∠A=∠C=90°,小亮想建一个圆形花坛,使四棵树都在花坛的边上.小亮请小明帮他设计方案: