题目内容
17.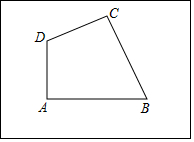 小亮家的房前有一块矩形的空地,空地上有四棵银杏树A、B、C,D,且∠A=∠C=90°,小亮想建一个圆形花坛,使四棵树都在花坛的边上.小亮请小明帮他设计方案:
小亮家的房前有一块矩形的空地,空地上有四棵银杏树A、B、C,D,且∠A=∠C=90°,小亮想建一个圆形花坛,使四棵树都在花坛的边上.小亮请小明帮他设计方案:(1)小明说:“过A、B、D三点作⊙O,点C一定在⊙O上”.你认为小明这种方法是否正确,若正确,请按照小明的方法,把花坛的位置画出来(尺规作图,不写作法,保留作图痕迹);并说明C点在⊙O上的依据;若不正确说明理由.
(2)若△ABD中,AD=6米,AB=8米,则小亮家圆形花坛的面积25π米2.
分析 (1)首先作出AD和AB的垂直平分线,两线的交点就是圆心O的位置,再以O为圆心,DO长为半径画圆即可;连接BD、CO,证明CO=DO即可;
(2)首先利用勾股定理计算出BD的长,进而可得⊙O的半径,再利用圆的面积公式进行计算即可.
解答 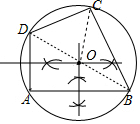 解:(1)小明说法正确,如图所示:
解:(1)小明说法正确,如图所示:
点C在⊙O上,
理由:连接BD、CO,
∵∠A=90°,
∴BD是⊙O的直径,
∵BO=DO,
∴点O是BD的中点,
∵∠DCB=90°,
∴CO=$\frac{1}{2}$BD,
∴CO=DO,
∴点C在⊙O上;
(2)∵AD=6米,AB=8米,
∴BD=$\sqrt{A{D}^{2}+A{B}^{2}}$=10(米),
∴DO=5米,
∴小亮家圆形花坛的面积为25π米2.
故答案为:25π.
点评 此题主要考查了作图--应用设计与作图,以及圆周角定理,勾股定理的应用,关键是掌握半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
7.y=-(x+1)2+k上有A(-$\sqrt{2}$,y1),B($\sqrt{2}$,y2)两点,则y1,y2的大小关系为( )
| A. | y1>y2 | B. | y1<y2 | C. | y1≥y2 | D. | y1≤y2 |
12.下列方程中,是关于x的一元二次方程的是( )
| A. | ax2+bx+c=0 | B. | x2-y-1=0 | C. | $\frac{1}{x}$+x=1 | D. | x2=2 |
9.从多边形的一个顶点出发,连接其它各个顶点得到2016个三角形,则这个多边形的边数为( )
| A. | 2015 | B. | 2016 | C. | 2017 | D. | 2018 |
 在如图所示的运算程序中,如果输出的数y=6,则输入的数x=2或9.
在如图所示的运算程序中,如果输出的数y=6,则输入的数x=2或9.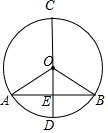 如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为E,交⊙O于点C、D,
如图所示,AB是⊙O的一条弦,OD⊥AB,垂足为E,交⊙O于点C、D,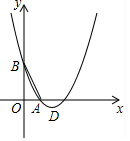 如图,已知抛物线y1=x2+bx+c经过A(1,0),B(0,2)两点,顶点为D.
如图,已知抛物线y1=x2+bx+c经过A(1,0),B(0,2)两点,顶点为D.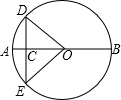 如图,C是⊙O直径AB上一点,过C作弦DE,使DC=OC,∠AOD=40°,求∠BOE的度数.
如图,C是⊙O直径AB上一点,过C作弦DE,使DC=OC,∠AOD=40°,求∠BOE的度数.