题目内容
19.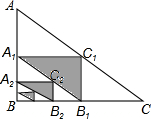 如图,Rt△ABC中,AB=6,BC=8,以AB,BC,AC的中点A1,B1,C1构成△A1B1C1,以A1B,BB1,A1B1的中点A2,B2,C2构成△A2B2C2…依次操作,阴影部分面积之和将接近( )
如图,Rt△ABC中,AB=6,BC=8,以AB,BC,AC的中点A1,B1,C1构成△A1B1C1,以A1B,BB1,A1B1的中点A2,B2,C2构成△A2B2C2…依次操作,阴影部分面积之和将接近( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
分析 先根据三角形面积公式得到Rt△ABC的面积,再根据三角形中位线定理得到△A1B1C1的面积,△A2B2C2的面积…,再根据等比数列求和公式可求阴影部分面积之和.
解答 解:∵Rt△ABC中,AB=6,BC=8,
∴Rt△ABC的面积为6×8÷2=24,
∵以AB,BC,AC的中点A1,B1,C1构成△A1B1C1,
∴△A1B1C1的面积是24×$\frac{1}{4}$=6,
∵以A1B,BB1,A1B1的中点A2,B2,C2构成△A2B2C2,
∴△A2B2C2的面积是24×$\frac{1}{4}$×$\frac{1}{4}$=1.5,
…,
∴阴影部分面积之和为$\frac{6-6×(\frac{1}{4})^{n-1}×\frac{1}{4}}{1-\frac{1}{4}}$=$\frac{6×(1-\frac{1}{4})^{n}}{\frac{3}{4}}$≈8.
故选:C.
点评 此题考查了三角形中位线定理,三角形面积,等比数列求和公式,关键是得到后面的阴影部分面积是前面阴影部分面积的$\frac{1}{4}$.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8.在数轴上与表示-3的点的距离等于2的点所表示的数是( )
| A. | 1 | B. | 5 | C. | 1或-2 | D. | -1或-5 |
9.已知点A(a,2016)与点B(2017,b)关于x轴对称,则a+b的值为( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
 如图,在△ABC中,∠ACB=116°,∠B=45°,CD平分∠ACB,CE为AB边上的高,求∠DCE的度数.
如图,在△ABC中,∠ACB=116°,∠B=45°,CD平分∠ACB,CE为AB边上的高,求∠DCE的度数. 如图,小明家(A点)在一条河流(直线l,宽度忽略不计)的一侧,在河流的同侧有一公园(B点),小风家恰好关于此河流与小明家对称
如图,小明家(A点)在一条河流(直线l,宽度忽略不计)的一侧,在河流的同侧有一公园(B点),小风家恰好关于此河流与小明家对称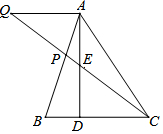 在△ABC中,AD是高,E是AD的中点,连接CE并延长交AB于点P,过点A作AQ∥BC,交CP的延长线于点Q,BD:CD:AD=1:2:3.
在△ABC中,AD是高,E是AD的中点,连接CE并延长交AB于点P,过点A作AQ∥BC,交CP的延长线于点Q,BD:CD:AD=1:2:3.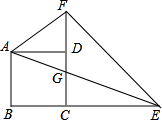 如图,已知正方形ABCD的边长为1,点E、F分别在边BC、CD的延长线上,AE与CD的交点为G,且∠EAF=45°.
如图,已知正方形ABCD的边长为1,点E、F分别在边BC、CD的延长线上,AE与CD的交点为G,且∠EAF=45°.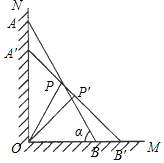 如图,一架长2米的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面的倾斜角α为60°.当A点下滑到A′点,B点向右滑行到B′点时,梯子AB的中点P也随之运动到P′点.若∠POP′=15°,则AA′的长$\sqrt{3}$-$\sqrt{2}$.
如图,一架长2米的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面的倾斜角α为60°.当A点下滑到A′点,B点向右滑行到B′点时,梯子AB的中点P也随之运动到P′点.若∠POP′=15°,则AA′的长$\sqrt{3}$-$\sqrt{2}$.