题目内容
9.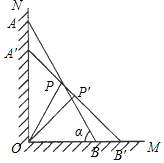 如图,一架长2米的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面的倾斜角α为60°.当A点下滑到A′点,B点向右滑行到B′点时,梯子AB的中点P也随之运动到P′点.若∠POP′=15°,则AA′的长$\sqrt{3}$-$\sqrt{2}$.
如图,一架长2米的梯子AB斜靠在与地面OM垂直的墙壁ON上,梯子与地面的倾斜角α为60°.当A点下滑到A′点,B点向右滑行到B′点时,梯子AB的中点P也随之运动到P′点.若∠POP′=15°,则AA′的长$\sqrt{3}$-$\sqrt{2}$.
分析 在Rt△AOB中,先求OB、OA的长,根据直角三角形斜边中线等于斜边一半可知:PA=PO,P′A′=P′O,由等边对等角得:∠AOP=∠PAO,∠OA′P′=∠A′OP′,由∠POP′=15°求得∠OA′P′=45°,根据三角函数求AA′=$\sqrt{3}$-$\sqrt{2}$.
解答 解:在Rt△AOB中,
∵∠AOB=90°,α=∠ABO=60°,
∴∠OAB=30°,
∴OB=$\frac{1}{2}$AB=$\frac{1}{2}$×2=1,OA=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$,
∵P、P′分别是AB、A′B′的中点,
∴PA=PO,P′A′=P′O,
∴∠AOP=∠PAO,∠OA′P′=∠A′OP′,
∴∠POP′=∠A′OP′-∠AOP=∠OA′P′-∠PAO,
∵∠POP′=15°
∴∠OA′P′-∠PAO=15°,
∵∠PAO=30°,
∴∠OA′P′=45°,
∴cos∠OA′P′=cos45°=$\frac{OA′}{A′B′}$,
∴OA′=$\frac{\sqrt{2}}{2}$×2=$\sqrt{2}$,
∴AA′=OA-OA′=$\sqrt{3}$-$\sqrt{2}$,
故答案为:$\sqrt{3}-\sqrt{2}$.
点评 本题是勾股定理的应用,考查了勾股定理在实际问题中的应用,本题是梯形问题,要明确无论梯形如何移动,梯子的长不变.

练习册系列答案
相关题目
19.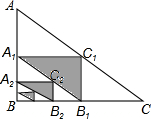 如图,Rt△ABC中,AB=6,BC=8,以AB,BC,AC的中点A1,B1,C1构成△A1B1C1,以A1B,BB1,A1B1的中点A2,B2,C2构成△A2B2C2…依次操作,阴影部分面积之和将接近( )
如图,Rt△ABC中,AB=6,BC=8,以AB,BC,AC的中点A1,B1,C1构成△A1B1C1,以A1B,BB1,A1B1的中点A2,B2,C2构成△A2B2C2…依次操作,阴影部分面积之和将接近( )
 如图,Rt△ABC中,AB=6,BC=8,以AB,BC,AC的中点A1,B1,C1构成△A1B1C1,以A1B,BB1,A1B1的中点A2,B2,C2构成△A2B2C2…依次操作,阴影部分面积之和将接近( )
如图,Rt△ABC中,AB=6,BC=8,以AB,BC,AC的中点A1,B1,C1构成△A1B1C1,以A1B,BB1,A1B1的中点A2,B2,C2构成△A2B2C2…依次操作,阴影部分面积之和将接近( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
17.下列函数中,不是二次函数的是( )
| A. | y=1-$\sqrt{2}$x2 | B. | y=2(x-1)2+4 | C. | y=$\frac{1}{2}$(x-1)(x+4) | D. | y=(x-2)2-x2 |
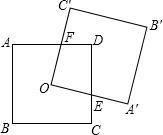 如图,正方形ABCD的对角线相交于点O,点O是正方形A′B′C′O的一个顶点.如果两个正方形的边长都等于2,那么正方形A′B′C′OA绕O点无论怎样转动,两个正方形重叠的部分的面积是1.
如图,正方形ABCD的对角线相交于点O,点O是正方形A′B′C′O的一个顶点.如果两个正方形的边长都等于2,那么正方形A′B′C′OA绕O点无论怎样转动,两个正方形重叠的部分的面积是1.