题目内容
7. 如图,在△ABC中,∠ACB=116°,∠B=45°,CD平分∠ACB,CE为AB边上的高,求∠DCE的度数.
如图,在△ABC中,∠ACB=116°,∠B=45°,CD平分∠ACB,CE为AB边上的高,求∠DCE的度数.
分析 由图知∠DCE=∠DCB-∠ECB,又由角平分线定义得∠DCB=$\frac{1}{2}$∠ACB,然后利用内角和定理,分别求出∠BCE即可.
解答 解:∵∠ACB=116°,CD平分∠ACB,
∴∠DCB=$\frac{1}{2}$∠ACB=58°.
∵CE⊥AB,
∴∠CEB=90°.
∵∠B=45°,
∴∠BCE=45°,
∴∠DCE=58°-45°=13°.
点评 本题考查的是三角形内角和定理,熟知三角形内角和是180°是解答此题的关键.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
16.下列代数式$\frac{1}{5}$a、2x2+2xy+y2、$\frac{a+1}{3}$、a2-$\frac{1}{b}$、-$\frac{1}{4}$(x+y)中多项式的个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.下列说法中正确的是( )
| A. | 任何正整数的因数至少有两个 | B. | 1是所有正整数的因数 | ||
| C. | 一个数的倍数总比它的因数大 | D. | 3的因数只有它本身 |
14.解为x=-3的方程是( )
| A. | 2x-6=0 | B. | 3(x-2)-2(x-3)=5x | C. | $\frac{3x+3}{2}$=6 | D. | $\frac{x-1}{4}$=$\frac{3-2x}{6}$-$\frac{5}{2}$ |
2.如图中的图①、②、③所示,阴影部分面积的大小关系正确的是( )


| A. | ①>②>③ | B. | ③>②>① | C. | ②>③>① | D. | ①=②=③ |
19.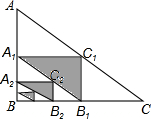 如图,Rt△ABC中,AB=6,BC=8,以AB,BC,AC的中点A1,B1,C1构成△A1B1C1,以A1B,BB1,A1B1的中点A2,B2,C2构成△A2B2C2…依次操作,阴影部分面积之和将接近( )
如图,Rt△ABC中,AB=6,BC=8,以AB,BC,AC的中点A1,B1,C1构成△A1B1C1,以A1B,BB1,A1B1的中点A2,B2,C2构成△A2B2C2…依次操作,阴影部分面积之和将接近( )
 如图,Rt△ABC中,AB=6,BC=8,以AB,BC,AC的中点A1,B1,C1构成△A1B1C1,以A1B,BB1,A1B1的中点A2,B2,C2构成△A2B2C2…依次操作,阴影部分面积之和将接近( )
如图,Rt△ABC中,AB=6,BC=8,以AB,BC,AC的中点A1,B1,C1构成△A1B1C1,以A1B,BB1,A1B1的中点A2,B2,C2构成△A2B2C2…依次操作,阴影部分面积之和将接近( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
16.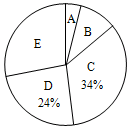 某市第三中学组织学生参加生命安全知识网络测试.小明对九年级2班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图.
某市第三中学组织学生参加生命安全知识网络测试.小明对九年级2班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图.
根据图表中的信息解答下列问题:
(1)求九年级2班学生的人数;
(2)写出频数分布表中a,b的值;
(3)已知该市共有80 000名中学生参加这次安全知识测试,若规定80分以上(含80分)为优秀,估计该市本次测试成绩达到优秀的人数;
(4)小明通过该市教育网站搜索发现,全市参加本次测试的中学生中,成绩达到优秀有56 320人.请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因.
 某市第三中学组织学生参加生命安全知识网络测试.小明对九年级2班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图.
某市第三中学组织学生参加生命安全知识网络测试.小明对九年级2班全体学生的测试成绩进行统计,并绘制了如图不完整的频数分布表和扇形统计图.根据图表中的信息解答下列问题:
(1)求九年级2班学生的人数;
(2)写出频数分布表中a,b的值;
(3)已知该市共有80 000名中学生参加这次安全知识测试,若规定80分以上(含80分)为优秀,估计该市本次测试成绩达到优秀的人数;
(4)小明通过该市教育网站搜索发现,全市参加本次测试的中学生中,成绩达到优秀有56 320人.请你用所学统计知识简要说明实际优秀人数与估计人数出现较大偏差的原因.
| 组别 | 分数段(x) | 频数 |
| A | 0≤x<60 | 2 |
| B | 60≤x<70 | 5 |
| C | 70≤x<80 | 17 |
| D | 80≤x<90 | a |
| E | 90≤x≤100 | b |
17.下列函数中,不是二次函数的是( )
| A. | y=1-$\sqrt{2}$x2 | B. | y=2(x-1)2+4 | C. | y=$\frac{1}{2}$(x-1)(x+4) | D. | y=(x-2)2-x2 |