题目内容
13.解方程(1)(x+5)2=121;
(2)2x2-2x-3=0.
分析 (1)两边开方,即可得出两个一元一次方程,求出方程的解即可;
(2)求出b2-4ac的值,再代入公式求出即可.
解答 解:(1)两边开方得:x+5=±11,
x+5=11,x+5=-11,
解得:x1=6,x2=-16;
(2)2x2-2x-3=0,
b2-4ac=(-2)2-4×2×(-3)=28,
x=$\frac{2±\sqrt{28}}{2×2}$,
x1=$\frac{1+\sqrt{7}}{2}$,x2=$\frac{1-\sqrt{7}}{2}$.
点评 本题考查了解一元二次方程的应用,能选择适当的方法解一元二次方程是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.一艘船在相距120千米的两个码头间航行,去时顺水用了4小时,回来时逆水用了5小时,则水速为( )
| A. | 2千米/小时 | B. | 3千米/小时 | C. | 4千米/小时 | D. | 5千米/小时 |
4.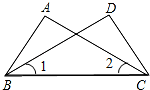 如图,已知∠ABC=∠DCB,下列条件中不能使△ABC≌△DCB的是( )
如图,已知∠ABC=∠DCB,下列条件中不能使△ABC≌△DCB的是( )
 如图,已知∠ABC=∠DCB,下列条件中不能使△ABC≌△DCB的是( )
如图,已知∠ABC=∠DCB,下列条件中不能使△ABC≌△DCB的是( )| A. | AB=DC | B. | AC=DB | C. | ∠1=∠2 | D. | ∠A=∠D |
1.用配方法解一元二次方程x2-4x-5=0,此方程可变形为( )
| A. | (x-2)2=9 | B. | (x+2)2=9 | C. | (x+2)2=1 | D. | (x-2)2=1 |
2.下列各图是由若干盆花组成的形如正方形的图案,每条边上(包括两个顶点)有n(n>1)盆花,每个图案花盆的总数是s,按图所示的图案回答下列问题.

(1)填表:
(2)当n=10时,s的值是多少?s是如何随n的变化而变化的?

(1)填表:
| n | 2 | 3 | 4 | 5 | 6 | … | n |
| s | 4 | 9 | 16 | 25 | 36 | … | n2 |
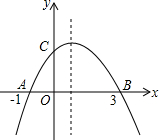 如图,二次函数y=ax2+bx+c的图象经过A (-1,0),B(3,0),C(0,3)两点.
如图,二次函数y=ax2+bx+c的图象经过A (-1,0),B(3,0),C(0,3)两点.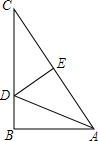 如图,Rt△ABC中,∠B=90°,AB=6,BC=8,现将△ABC翻折,使点C与点A重合,折痕为DE,求CD及DE的长.
如图,Rt△ABC中,∠B=90°,AB=6,BC=8,现将△ABC翻折,使点C与点A重合,折痕为DE,求CD及DE的长.