题目内容
2.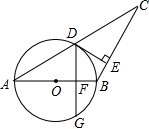 如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为A.作DG⊥AB交⊙O于G,垂足为F,若∠A=30°,AB=8.
如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为A.作DG⊥AB交⊙O于G,垂足为F,若∠A=30°,AB=8.(1)求弦DG的长.
(2)求证:DE是⊙O的切线.
分析 (1)求DG就是求DF的长,在直角三角形DFO中,有OD的值,∠DOF的值也容易求得,那么DG的值就求得了;
(2)连接OD,只要证明OD⊥DE即可.本题可根据等腰三角形中两底角相等,将相等的角进行适当的转换,即可证得OD⊥DE.
解答 (1)解:∵∠DOF=∠A+∠ADO=60°,
在Rt△DOF中,OD=4,
∴DF=OD•sin∠DOF=4•sin60°=2$\sqrt{3}$.
∵直径AB⊥弦DG,
∴DF=FG.
∴DG=2DF=4$\sqrt{3}$;
(2)证明:连接OD,
∵OA=OD,
∴∠A=∠ADO.
∵BA=BC,
∴∠A=∠C,
∴∠ADO=∠C,
∴DO∥BC.
∵DE⊥BC,
∴DO⊥DE.
∵点D在⊙O上,
∴DE是⊙O的切线.
点评 本题考查了切线的判定,垂径定理等知识点.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.下列汉字中,是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
12.若等腰三角形中有一个角等于70°,则这个等腰三角形的顶角的度数是( )
| A. | 70° | B. | 40° | C. | 70°或40° | D. | 70°或55° |

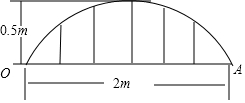 某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m 加设不锈钢管(如图)做成立柱.为了计算所需不锈钢管立柱的总长度,设计人员测得如图所示的数据.
某公司草坪的护栏是由50段形状相同的抛物线组成的,为牢固起见,每段护栏需按间距0.4m 加设不锈钢管(如图)做成立柱.为了计算所需不锈钢管立柱的总长度,设计人员测得如图所示的数据.