题目内容
2．已知m满足$\left\{\begin{array}{l}{2x+3y-m=0}\\{3x+2y+1+2m=0}\end{array}\right.$，且$\sqrt{x+y-2016}$=-$\sqrt{2016-x-y}$，求m的值．分析 根据已知等式求出x+y的值，原方程①+②后，再两边同除5，得到用m表示x+y的式子，求出m的值．
解答 解：∵$\sqrt{x+y-2016}$=-$\sqrt{2016-x-y}$，
∴x+y≥2016，x+y≤2016，
即x+y=2016
$\left\{\begin{array}{l}{2x+3y-m=0①}\\{3x+2y+1+2m=0②}\end{array}\right.$
（①+②）÷5得，
x+y=-$\frac{1+m}{5}$，
-$\frac{1+m}{5}$=2016
m=-10081
点评 本题考查的是二元一次方程组的解法和非负数的性质，运用算术平方根的性质求出x+y的值是解题的关键，解方程组时，根据方程组的特点，运用整体思想解答比较简单．
练习册系列答案
阅读快车系列答案
相关题目
13．已知x=$\sqrt{3}$+1，则x2-2x+3的值是（ ）
| A． | 4 | B． | 9 | C． | 5 | D． | 6 |
10．下列各组根式是同类二次根式的是（ ）
| A． | 2$\sqrt{2}$和$\sqrt{\frac{1}{2}}$ | B． | $\sqrt{2}$和$\sqrt{{2}^{2}}$ | C． | $\sqrt{{a}^{2}b}$与$\sqrt{a{b}^{2}}$ | D． | $\sqrt{4a}$与$\sqrt{2{a}^{2}}$ |
17．当a=3，b=2时，（$\sqrt{\frac{1}{a}}$-$\sqrt{b}$）$\sqrt{ab}$的值为（ ）
| A． | $\sqrt{2}-2\sqrt{3}$ | B． | $\sqrt{6}$ | C． | $\sqrt{10}$ | D． | $\sqrt{2}-\sqrt{12}$ |
7．下列说法正确的是（ ）
| A． | 哥哥的身高比弟弟高是必然事件 | |
| B． | 今年中秋节有雨是不确定事件 | |
| C． | 随机抛一枚均匀的硬币两次，都是正面朝上是不可能事件 | |
| D． | “彩票中奖的概率为$\frac{1}{5}$”表示买5张彩票肯定会中奖 |
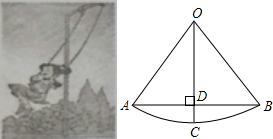如图，小丽荡秋千，秋千链子的长OA为2.5米，秋千向两边摆动的角度相同，摆动的水平距离AB为3米，则秋千摆至最高位置时与最低价位置时的高度之差（即CD）为0.5米．
如图，AD、BE是△ABC的中线，则下列结论中，正确的个数有（ ）