题目内容
12．下列说法不正确的是（ ）| A． | $\sqrt{a}$（a≥0）是二次根式 | B． | 当a＜0时，（$\sqrt{a}$）2=-a | ||
| C． | $\sqrt{{a}^{2}+b}$是最简二次根式 | D． | $\sqrt{（x+3）^{2}}$=x+3成立的条件是x＞-3 |
分析 判定一个二次根式是不是最简二次根式的方法，就是逐个检查最简二次根式的两个条件是否同时满足，同时满足的就是最简二次根式，否则就不是．
解答 解：A、$\sqrt{a}$（a≥0）是二次根式，故A正确；
B、被开方数不能小于零，故B错误；
C、被开方数不含分母；被开方数不含能开得尽方的因数或因式，故C正确；
D、$\sqrt{（x+3）^{2}}$=x+3成立的条件是x＞-3，故D正确；
故选：B．
点评 本题考查最简二次根式的定义．根据最简二次根式的定义，最简二次根式必须满足两个条件：被开方数不含分母；被开方数不含能开得尽方的因数或因式．
练习册系列答案
相关题目
如图，点P是菱形ABCD的对角线DB的延长线上一点，连接PC并延长，交AD的延长线于E，AB的延长线交PC于点F．
17．当a=3，b=2时，（$\sqrt{\frac{1}{a}}$-$\sqrt{b}$）$\sqrt{ab}$的值为（ ）
| A． | $\sqrt{2}-2\sqrt{3}$ | B． | $\sqrt{6}$ | C． | $\sqrt{10}$ | D． | $\sqrt{2}-\sqrt{12}$ |
4．
如图所示的几何体是由4个小正方体搭成，则它的主视图是（ ）
如图所示的几何体是由4个小正方体搭成，则它的主视图是（ ）| A． |  | B． |  | C． |  | D． |  |
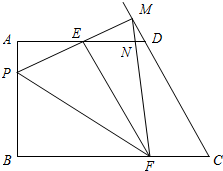已知：如图，在梯形ABCD中，AD∥BC，AB⊥BC，E是上底AD的中点，P是腰AB上一动点，联结PE并延长，交射线CD于点M，作EF⊥PE，交下底BC于点F，联结MF交AD于点N，联结PF，AB=AD=4，BC=6，点A、P之间的距离为x，△PEF的面积为y．