题目内容
5．如果点P（1+a，2a-1）在平面直角坐标系的第四象限内，那么a的取值范围在数轴上可表示为（ ）| A． |  | B． |  | C． |  | D． |  |
分析 根据第四象限内的点横坐标大于零，纵坐标小于零，可得不等式组，然后解不等式组，可得答案．
解答 解：由点P（1+a，2a-1）在平面直角坐标系的第四象限内，得
$\left\{\begin{array}{l}{1+a＞0}\\{2a-1＜0}\end{array}\right.$．
解得：-1＜a＜0.5，
故选B．
点评 本题考查了解一元一次不等式组，点的坐标以及在数轴上表示不等式的解集，熟记各象限内点的坐标特点是解题关键．
练习册系列答案
相关题目
15．若xy＜0，则$\sqrt{（{x}^{2}+{y}^{2}）^{2}-（{x}^{2}-{y}^{2}）^{2}}$的值是（ ）
| A． | 2 | B． | -2 | C． | 2xy | D． | -2xy |
16．下列每组中的两个代数式，不属于同类项的是（ ）
| A． | $\frac{1}{2}$x2y与$\frac{2}{3}$xy2 | B． | $\frac{1}{2}$m3n与-8nm3 | C． | -3与π | D． | 0.5a2b与πa2b |
如图，△ABC中，AB=AC=10，AD平分∠BAC交BC于点D，点E为AC的中点，连接DE，则DE的长为（ ）
如图所示，AD是△ABC的角平分线，EF平分AD，分别交AB于E，交AC于F，则四边形AEDF是菱形吗？请说明理由．
如图，在矩形ABCD中，AB=$\sqrt{19}$，AD=8，点P、Q分别是AD边和BC边上的动点，点P从点A向点D运动，点Q从点C向点B运动，且保持CQ=2AP，设AP=x．
14．下列“表情图”中，可以看作是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
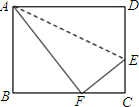如图，折叠长方形的一边AD，使点D落在BC边上的F点处，若AB=8cm，BC=10cm，则EC长为3cm．