题目内容
16．
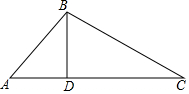如图，在△ABC中，∠ABC=120°，BD是AC边上的高，若AB+AD=DC，则∠C等于20°．
分析 延长DA到E，使AE=AB，从而求出DE=DE，然后根据线段垂直平分线上的点到线段两端点的距离相等可得BC=BE，再根据等边对等角可得∠C=∠E，∠E=∠ABE，再根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠BAD，然后根据三角形的内角和定理列式计算即可得解．
解答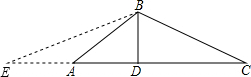 
解：如图，延长DA到E，使AE=AB，
∵AB+AD=DC，
∴AE+AD=AB+AD=DC，
又∵BD是AC边上的高，
∴BD是CE的垂直平分线，
∴BC=BE，
根据等边对等角，∠C=∠E，∠E=∠ABE，
根据三角形的外角性质，∠BAD=∠E+∠ABE=2∠C，
在△ABC中，∠BAD+∠C+∠ABC=180°，
∴2∠C+∠C+120°=180°，
解得∠C=20°．
故答案为：20°．
点评 本题考查了等腰三角形的判定与性质，线段垂直平分线上的点到线段两端点的距离相等的性质，利用“补长”法作辅助线构造出等腰三角形是解题的关键．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
如图是一个长方形推拉窗，窗高1.5米．当活动窗扇拉开长度b（米）时，长方形窗框的通风面积为1.5b米2．
7．对一批衬衣进行抽检，统计合格衬衣的件数，得到合格衬衣的频数表如表：
估计任抽一件衬衣是合格品的概率0.95．
| 抽取件数（件） | 50 | 100 | 200 | 500 | 800 | 1000 |
| 合格频数 | 47 | 93 | 189 | 489 | 760 | 950 |
如图，已知在△ABC中，D为AC中点，连接BD．
如图，在△ABC中，∠B=90°，AB=6cm，BC=8cm，动点P从点A开始沿AB边向B以1cm/s的速度移动（不与点B重合）；动点Q从B点开始沿BC边向点C以2cm/s的速度移动（不与点C重合）．如果P、Q分别从A、B同时出发，出发多少秒后，四边形APQC的面积为16cm2？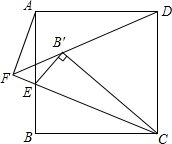
如图，E为正方形ABCD边AB上的一点，且AB=3，BE=1．将△CBE翻折得到△CB'E，连接并延长DB'与CE延长线相交于点F，连接AF，则AF的长为$\frac{3\sqrt{10}}{5}$．
如图，从一个棱长为3cm的正方体的一顶点处挖去一个棱长为1cm的正方体，则剩余部分的表面积是54cm2．