题目内容
8.若关于x的不等式组$\left\{\begin{array}{l}{3x-1>a+1}\\{2-x>1-2a}\end{array}\right.$无解,求a的取值范围.分析 先把a当作已知条件求出不等式组的解集,再与已知不等式组无解相比较即可得出实数a的取值范围.
解答 解:解不等式3x-1>a+1,得:x>$\frac{a+2}{3}$,
解不等式2-x>1-2a,得:x<1+2a,
∵不等式组无解,
∴$\frac{a+2}{3}≥1+2a$,
解得:a≤-$\frac{1}{5}$.
故a的取值范围是a≤-$\frac{1}{5}$.
点评 本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
20.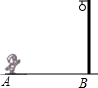 如图,小强晚上在路灯下散步,在由A处走到B处这一过程中,他在地上的影子( )
如图,小强晚上在路灯下散步,在由A处走到B处这一过程中,他在地上的影子( )
 如图,小强晚上在路灯下散步,在由A处走到B处这一过程中,他在地上的影子( )
如图,小强晚上在路灯下散步,在由A处走到B处这一过程中,他在地上的影子( )| A. | 逐渐变短 | B. | 逐渐变长 | C. | 先变短后变长 | D. | 先变长后变短 |
18.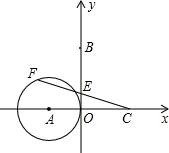 如图,在平面直角坐标系中,A(-5,0),B(0,10),C(8,0),⊙A的半径为5.若F是⊙A上的一个动点,线段CF与y轴交于E点,则△CBE面积的最大值是( )
如图,在平面直角坐标系中,A(-5,0),B(0,10),C(8,0),⊙A的半径为5.若F是⊙A上的一个动点,线段CF与y轴交于E点,则△CBE面积的最大值是( )
 如图,在平面直角坐标系中,A(-5,0),B(0,10),C(8,0),⊙A的半径为5.若F是⊙A上的一个动点,线段CF与y轴交于E点,则△CBE面积的最大值是( )
如图,在平面直角坐标系中,A(-5,0),B(0,10),C(8,0),⊙A的半径为5.若F是⊙A上的一个动点,线段CF与y轴交于E点,则△CBE面积的最大值是( )| A. | $\frac{160}{3}$ | B. | 40 | C. | 20 | D. | $\frac{40}{3}$ |
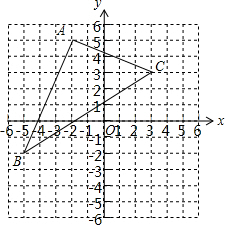 如图,已知△ABC各顶点的坐标分别为A(-2,5)B(-5,-2),C(3,3).将△ABC先向右平移4个单位长度,再向下平移3个单位长度,得到△A′B′C′.
如图,已知△ABC各顶点的坐标分别为A(-2,5)B(-5,-2),C(3,3).将△ABC先向右平移4个单位长度,再向下平移3个单位长度,得到△A′B′C′.