题目内容
9．
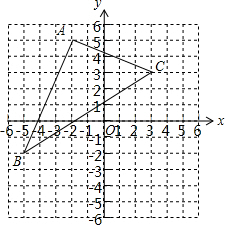如图，已知△ABC各顶点的坐标分别为A（-2，5）B（-5，-2），C（3，3）．将△ABC先向右平移4个单位长度，再向下平移3个单位长度，得到△A′B′C′．（1）在图中画出第二次平移之后的图形△A′B′C′；
（2）如果将△A′B′C′看成是由△ABC经过一次平移得到的，请指出这一平移的平移方向和平移距离．
分析 （1）根据平移的性质画出图形即可；
（2）连接AA′，根据勾股定理求出AA′的长，进而可得出结论．
解答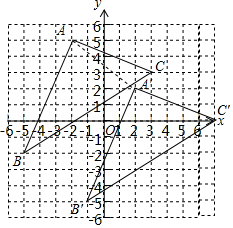 
解：（1）△A′B′C′如图所示；
（2）连接AA′，∵由图可知，AA′=$\sqrt{{3}^{2}+{4}^{2}}$=5，
∴如果将△A′B′C′看成是由△ABC经过一次平移得到的，那么这一平移的平移方向是由A到A′的方向，平移的距离是5个单位长度．
点评 本题考查的是作图-平移变换，熟知图形平移不变性的性质是解答此题的关键．
练习册系列答案
阅读快车系列答案
相关题目
已知一次函数与反比例函数的图象交于P（-3，m），Q（2，-3）．
4．
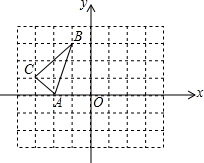如图，在直角坐标系xOy中，△ABC的三个顶点都在方格纸的格点上，点A的坐标是（-2，0），将△ABC绕点A顺时针旋转90°得到△AB′C′，则点B的对应点B′的坐标是（ ）
如图，在直角坐标系xOy中，△ABC的三个顶点都在方格纸的格点上，点A的坐标是（-2，0），将△ABC绕点A顺时针旋转90°得到△AB′C′，则点B的对应点B′的坐标是（ ）| A． | （1，-1） | B． | （1，1） | C． | （-1，1） | D． | （-1，-1） |
1．向量（$\overrightarrow{AB}$+$\overrightarrow{MB}$）+（$\overrightarrow{BO}$+$\overrightarrow{BC}$）+$\overrightarrow{OM}$化简后的结果等于（ ）
| A． | $\overrightarrow{BC}$ | B． | $\overrightarrow{AB}$ | C． | $\overrightarrow{AC}$ | D． | $\overrightarrow{AM}$ |