题目内容
10.先化简:($\frac{1}{a}$-$\frac{2}{a-1}$)÷$\frac{a^2+a}{1-2a+a^2}$,再从1、-1、0和$\sqrt{2}$选取一个合适的数作为a的值代入求值.分析 先将原式化简,然后将a=$\sqrt{2}$代入化简后的式子,即可求得相应的值,注意本题的原式要有意义,则分母不等于0,除式不等于0,从而可以发现a不等于1、-1、0.
解答 解:($\frac{1}{a}$-$\frac{2}{a-1}$)÷$\frac{a^2+a}{1-2a+a^2}$
=$\frac{a-1-2a}{a(a-1)}×\frac{(a-1)^{2}}{a(a+1)}$
=$\frac{-(a+1)}{a(a-1)}×\frac{(a-1)^{2}}{a(a+1)}$
=$\frac{1-a}{{a}^{2}}$,
当a=$\sqrt{2}$时,原式=$\frac{1-\sqrt{2}}{(\sqrt{2})^{2}}$=$\frac{1-\sqrt{2}}{2}$.
点评 本题考查分式的化简求值,解题的关键是明确题意,选取合适的a的值,注意挖掘题目中的隐含条件,原式中的分母和除式都不等于0.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
1.向量($\overrightarrow{AB}$+$\overrightarrow{MB}$)+($\overrightarrow{BO}$+$\overrightarrow{BC}$)+$\overrightarrow{OM}$化简后的结果等于( )
| A. | $\overrightarrow{BC}$ | B. | $\overrightarrow{AB}$ | C. | $\overrightarrow{AC}$ | D. | $\overrightarrow{AM}$ |
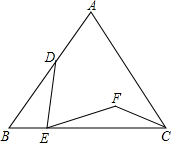 如图,在等边△ABC中,D、E分别为AB、BC边上的动点,满足AD=2BE,将线段DE绕点E顺时针旋转60°得线段EF,求证:CF平分∠ACB.
如图,在等边△ABC中,D、E分别为AB、BC边上的动点,满足AD=2BE,将线段DE绕点E顺时针旋转60°得线段EF,求证:CF平分∠ACB.